How to measure tiny temperature differences using a Josephson junction

At low temperatures, the resistivity of a metal (the inverse of its conductivity) is nearly constant. As the temperature of a material is lowered and as we approach absolute zero the resistivity should approach a constant value. Many metals, known as normal metals, behave in this way.

The behaviour of another class of metals and some other materials is quite different. These metals behave normally as the temperature is decreased, but at some critical temperature (which depends on the properties of the metal), the resistivity drops suddenly to zero. These materials are known as superconductors. The resistivity of a superconductor is not merely very small at temperatures below the critical temperature; it vanishes! Such materials can conduct electric currents even in the absence of an applied voltage, and the conduction occurs with no joule heating losses.

Conspicuously absent from the list of superconductors are the best metallic conductors (Cu, Ag, Au), which suggests that superconductivity is not caused by a good conductor getting better but instead must involve some fundamental change in the material. In fact, superconductivity results from a kind of paradox: ordinary materials can be good conductors if the electrons have a relatively weak interaction with the lattice, but superconductivity results from a strong interaction between the electrons and the lattice.

Consider an electron moving through the lattice. As it moves, it attracts the positive ions and disturbs the lattice, much as a boat moving through water creates a wake. These disturbances propagate as lattice vibrations, which can then interact with another electron. In effect, two electrons interact with one another through the intermediary of the lattice; the electrons move in correlated pairs (called Cooper pairs) that do not lose energy by interacting with the lattice.

Imagine now a thin layer of insulating material sandwiched between two identical superconductors. If we had normal metals at each side the insulator would stop any current flowing between them. But this is not the case with superconductors. If the insulating layer is thin enough the electron pairs can tunnel through from one superconductor to another. This is a typical case of one-dimensional barrier penetration, usually called quantum mechanical tunnelling. Classically, the particles should never appear at the other side, because they do not have sufficient energy to overcome the barrier. But this phenomenon of penetration of a forbidden region is a well-known property of classical waves. Quantum physics provides a new aspect to this phenomenon by associating a particle with the wave, and thus allowing a particle to pass through a classically forbidden region.

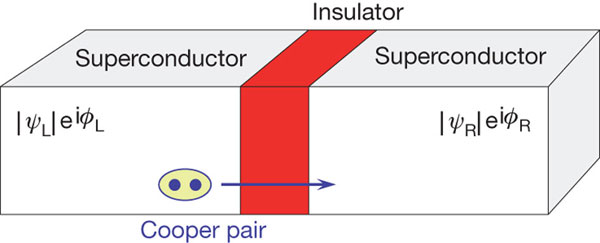
As electron behaviour is described then by a wave function, the current through this junction depends on a phase angle which is the difference between the phases in the two superconducting pieces. The existence of this “supercurrent” through the junction was first predicted by Brian Josephson in 1969, and it is now known as the Josephson effect. Josephson shared the 1973 Nobel Prize in physics for this discovery.

The Josephson effect and the Josephson junction have found multiple applications in quantum-mechanical circuits, like SQUIDs, superconducting qubits, and RSFQ digital electronics.

Now a group of researchers, that includes Sebastián Bergeret from the Materials Physics Center (CSIC/EHU) and DIPC, predicts¹ theoretically that applying a temperature gradient to a Josephson junction where the insulating material is composed of two layers, a permanent magnet and a nonmagnetic one, may result in an effect (called a thermophase) several orders of magnitude larger than that predicted to occur in conventional Josephson junctions. The result, published in Physical Review Letters, could allow the manufacturing of ultrasensitive radiation detectors.

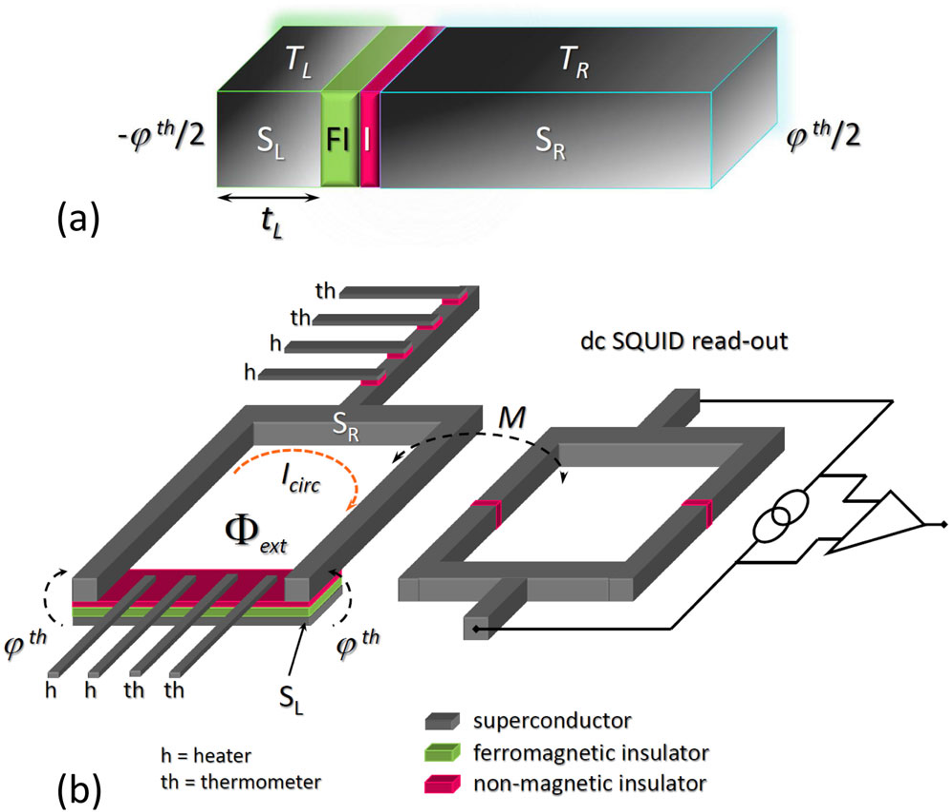
The concept of thermophase refers to the appearance of a phase gradient inside of a superconductor due to a temperature gradient across it. The differences in phases are in the origin of supercurrents, as we mentioned earlier, and this supercurrents can balance the current of quasiparticles induced by the difference in temperatures.

The total electric current flowing throuh the junction is the result of the sum of the quasiparticle and the Josephson contributions. In an electrically open configuration (no closed circuits) the total charge current has to vanish, implying that the quasiparticle contribution and the Josephson one have to cancel each other. This cancellation is the origin of the thermophase as the Josephson contribution depends on the phase angle. Thus, the thermophase (the phase angle at which the cancellation occurs) is a measure of the amplitude of the thermoelectric effect at the contact between superconductors.

The researchers think that it is physically feasible to build a device to measure this effect with existing materials and technologies. An effect that can be as high as π/2, which is huge compared to that of a conventional Josephson junction (0,0001). This sharp response combined with the low heat capacity of superconductors could be used to build devices for detecting tiny temperature differences, where the radiation induced heating of the superconductors is detected via the termophase.

Author: César Tomé López is a science writer and the editor of Mapping Ignorance.