Micro black holes are seeds of vacuum instability

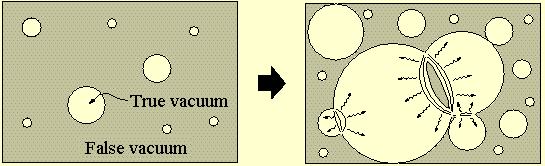
Our universe is not stable according to the currently measured values of the top quark and Higgs particle masses. There is a non-null probability that at any instant in the next billions of years the present “false vacuum” will change to a “true vacuum” by quantum tunneling, destroying all matter, energy and spacetime without any forewarning. Theoretically, a first-order phase transition will occur by bubble nucleation. Usually, phase transitions are dominated by bubbles nucleating around fixed sites, like impurities in the medium or imperfections in the containment vessel. Philipp Burda, from Durham University, U.K., and two colleagues have studied the effect of quantum gravity corrections added to the Higgs potential during the vacuum instability phase transition ¹. Their result is amazing, small black holes can act as nucleation seeds for the decay of the metastable vacuum.

In the standard model all the parameters change with the energy scale µ. The Higgs field has a quartic potential V(h) ≈ λ(µ) h⁴ with a positive coupling λ(m_H) at the electroweak scale µ ≈ m_H. Assuming that no physics beyond the standard model of particle physics exists between the electroweak and the Planck scale, the renormalization group equations show that λ(µ) becomes negative for µ about 10¹⁰ GeV. Hence, there is a new lower-energy vacuum, a true vacuum, and our universe lives in a metastable (false) vacuum. The very small probability of quantum tunneling between the false and the true vacua is such that the lifetime of our vacuum is longer than the age of the universe ². Current experimental uncertainties in the top quark and Higgs particle are large, so this vacuum metastability could be only apparent. Moreover, there may be physics beyond the standard model of particle physics that could stabilize the universe.

The instability of the vacuum is a first-order phase transition as shown by Coleman and de Luccia ³. This kind of phase transition occurs by bubble nucleation. The formation of a bubble costs energy because a wall with energy and tension is formed as a barrier between the false and true vacua. This energy is balanced by that gained by the volume of true vacuum inside the bubble. Hence, there is a non-null probability that by quantum tunneling (an instanton solution) a lower-energy vacuum bubble come to exist by chance. Once the bubble forms its growing is energetically favorable and it expands at nearly the speed of light destroying everything around.

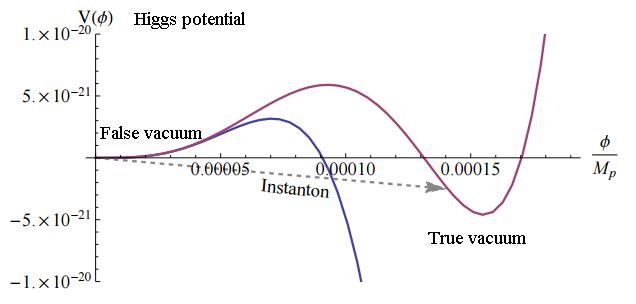
The analysis of the stability of the vacuum of our universe is based on the standard model without taking into account the gravitational interaction. We still do not have the final version of the quantum theory of gravity, so Burda and colleagues used an effective quantum field theory to extend the results of Coleman and de Luccia under the thin-wall approximation for the vacuum bubbles. They found a critical mass for the black holes, around 10-100 times the Planck mass, such that a bubble nucleates outside the black hole replacing it with true vacuum. The critical mass results from the vacuum decay rate exceeding the Hawking evaporation rate for the black hole. In fact, micro black holes can massively speed up the rate of decay of a metastable Higgs vacuum by acting as nucleation sites.

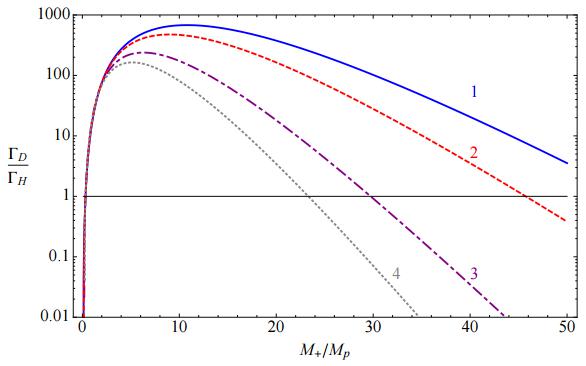
The analysis of Burda and colleagues is preliminary, based in the thin-wall approximation for the vacuum bubble and an effective theory for modified Higgs potential under gravity. Figure 2 shows that for a large family of models the false vacuum nucleation rate exceeds the Hawking evaporation rate for micro black holes with masses of tens of the Planck mass. The analysis requires several assumptions. In an unpublished preprint ⁴ these authors have considered an analysis beyond the thin-wall approximation. For thick-wall bubbles the main conclusions do not change, hence they are robust under small parameter uncertainties. However, further numerical studies of the Higgs potential parameter space are necessary to understand whether the result is just an issue for a small corner of parameter space or the effect are pervasive across the whole metastable region of the Higgs potential.

In summary, the presence of any micro black holes may eventually trigger a catastrophic phase transition from our standard model. The analytic results of Burda and colleagues serve as a proof of principle that the issue of metastability of our universe may not be as simple as initially was thought.