The uncertainty principle, under a new light
In ordinary life it is assumed that any physical property of an object can be measured as accurately as necessary. To reach any desired degree of accuracy would require only a sufficiently precise instrument. Wave mechanics showed, however, that even in thought experiments with ideal instruments there are limits to the accuracy of measurements that can be achieved.

For example, think how you would go about measuring the positions and velocity of a car moving slowly along a road. You could mark the position of the front end of the car at a given instant by making a scratch on the ground. At the same time, you could start a stopwatch. Then you could run to the end of the road, where you have previously placed another mark. At the instant when the front of the car reaches this point, you stop the watch. You then measure the distance between the marks and get the average speed of the car by dividing the distance travelled by the time elapsed. Since you know the direction of the car’s motion, you know the average velocity. Thus, you know that at the moment the car reached the second mark it was at a certain distance from its starting point and had travelled at a certain average velocity. By going to smaller and smaller intervals, you could also get the instantaneous velocity at any point along its path.
How did you get the needed information? You located the car by sunlight that was bounced off the front end into your eyes. The light permitted you to see when the car reached a mark on the ground. To get the average speed, you had to locate twice where the front end was.
But suppose that you had decided to use reflected radio waves instead of visible light. At 1000 kHz, a typical value for radio signals, the wavelength is 300 m. This wavelength is very much greater than the dimensions of the car. Thus, it would be impossible to locate the position of the car with any accuracy. The wave would reflect from the car (“scatter” is a better term) in all directions. It would also sweep around any human-sized device you may wish to use to detect the wave direction. The wavelength has to be comparable with or smaller than the dimensions of the object before the object can be located well.
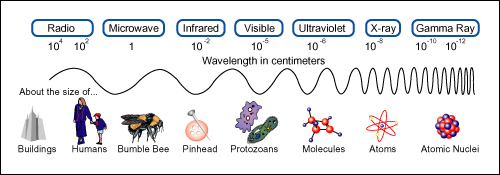
Radar uses wavelengths from about 0.1 cm to about 3 cm, so a radar apparatus could be used instead of sunlight. But even radar would leave uncertainties as large as several centimeters in the two measurements of position. The wavelength of visible light is less than 10-6 m. For visible light, then, you could design instruments that would locate the position of the car to an accuracy of a few thousandths of a millimetre.
Now think of an electron moving along an evacuated tube. You will try to measure the position and speed of the electron. But you must change your method of measurement. The electron is so small that you cannot locate its position by using ordinary visible light. (The wavelength of visible light, small as it is, is still at least 104 times greater than the diameter of an atom.)
You are attempting to locate the electron within a tiny region, say the size of an atom, about 10-10 m across. So you need a light beam whose wavelength is about 10-10 m or smaller. But a photon of such a short wavelength (and high frequency f ) has very great momentum (h/λ) and energy (hf ). Such a photon will give the electron a strong kick when it is scattered by the electron. As a result, the velocity of the electron will be greatly changed, into a new and unknown direction. This is a new problem, one you did not even think about when measuring the position of the car! Therefore, when you receive the scattered photon, you can deduce from its direction where the electron once was; in this sense you can “locate” the electron. But in the process you have changed the velocity, hence the momentum, of the electron (in both magnitude and direction). In short, the more accurately you locate the electron by using photons of shorter wavelength, the less accurately you can know its momentum.
You could try to disturb the electron less by using less energetic photons. But because light exists in quanta of energy hf, a lower-energy photon will have a longer wavelength. This would create greater uncertainty about the electron’s position!
In other words:
It is impossible to measure both the position and the momentum of a subatomic particle, in the same instant to unlimited accuracy. The more accurate is the measurement of the momentum, the less accurate is the measurement of the position in that instant, and vice versa.
This conclusion is the uncertainty principle, first stated by Werner Heisenberg in 1927.
Author: César Tomé López is a science writer and the editor of Mapping Ignorance
1 comment
That was a terrific explanation. But I’m a little confused. I have read that shorter wavelengths scatter more than longer ones, and Radio waves have longer wavelengths than visible light. Would I be right in understanding that although visible light scatters more than radio waves, it is possible to locate the car in the former simply because the wavelength is smaller than the car (just like how you need a ruler with smaller divisions than the thing you’re measuring)? Does the fact that radio waves don’t serve the purpose have anything to do with the fact that they scatter? Or is it that they bend around the obstacles and hence can’t be used to measure location, since you have mentioned both the scattering and the bending?
(Forgive me if I’m sounding dumb here, but I just couldn’t help trying to clear my doubts.)