Family unification (1)
Our core theory of fundamental physics, the Standard Model (SM), describes a vast range of phenomena precisely and very accurately. In that sense it is close to Nature’s last word. It presents, however, some shortcomings. For example, the SM contains three different forces and many independent fields. It is attractive to imagine that a deeper unity underlies this observed multiplicity.

Thanks to the gauge principle, in Quantum Field Theory interactions are codified into symmetry groups, under which our theory must be locally invariant. Our most fundamental theory, the SM, is based in the symmetry SU(3)xSU(2)xU(1). The three independent groups encode three different interactions, i.e. the strong, weak and electromagnetic forces. Additionally, when coming to fermions, it contains a plethora of independent components: each family contains two quarks (with charges +2/3 and -1/3) that come in three colors, one lepton with charge -1 and one neutral lepton called neutrino. Moreover, for some unknown reason, in Nature this family structure is triplicated.
During the 70s, some physicists proposed 12 that the apparently independent forces are unified at high energies in a unique interaction represented as a simple gauge group. Additionally, quantum corrections explain why at low energies the strength of SM interactions are so different. These theories are usually known as Grand Unified Theories, GUT.
Even more important than these nice features, one property of GUTs is that there exist connections between quarks and leptons: they belong to the same multiplet of the gauge group. Phenomenologically this means that the unified interaction can convert a quark into a lepton and vice-versa. These transitions can mediate the decay of protons (which in the SM are stable), making this process the smoking gun of GUTs. However, the rate of proton decay is highly suppressed due to the breaking, at very high energies, of the initial symmetry down to the SM.
Unfortunately, while unifying interactions is quite straightforward a unified description of all the elementary fermions, a theory that in addition to forces also unifies families, is not an easy task. There are several difficulties one must overcome in order to build a consistent theory of family unification. One of them is related with the quantum consistency of the theory, i.e. one has to deal with gauge anomalies. These anomalies are dangerous because they break gauge symmetry at the quantum level and also may spoil renormalizability of the theory.
In addition to a simple group that contains the Standard Model, the gauge group of a family unification theory must contain representations that are able to accommodate the family structure and its replication. This constraints severely our possibilities, since unitary groups, SU(N), able to accommodate the SM chirality usually lead to anomalies. Fortunately, there exist another possibility that consist on the orthogonal groups: SO(N). This groups, except for N=6, are anomaly free and, strikingly, for some special values of N these groups can reproduce chirality. Other interesting choice is the exceptional group E6, but its 27 representation contains only one family.
The anomaly free condition suggest that it is interesting to study the groups SO(4n+2) because, as we have said, in addition to anomaly freedom they can also reproduce chirality. These groups have a chiral spinor representation with dimension 22n. Other property that justifies this election is that, unlike tensor representations, spinors decompose repetitively when breaking the symmetry group down to a smaller group. Can this property of spinors explain the family repetition?
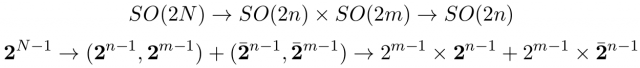
Inspired by these properties, in the 80s M. Gell-Mann, P. Ramond and R. Slansky 3, Y. Fujimoto 4 and, independently, F. Wilczek and A. Zee 5 proposed to use a unified theory based in SO(18) and its 256-dimensional spinor representation. The reason for this choice is that SO(18) contains the smallest spinor able to contain, at least, three left-handed families (one has to keep in mind that the SM weak interaction is left-handed). However, this spinor turns out to be too large. This fact can be seen from the symmetry breaking to SO(10):
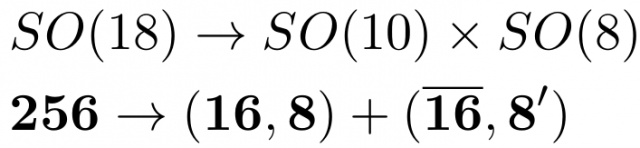
Where each 16 is the spinor representation of SO(10) that when breaking the symmetry down to the SM it splits as
![]()
Since each 16-dimensional spinor of SO(10) contains one family, the 256 spinor contains 8 families and also 8 mirror families (families with the opposite chirality, this is right-handed). This proliferation of families is a tough phenomenological problem: we only observe 3 families and, moreover, these families are left-handed.
In order to get rid of the extra families Gell-Mann, Ramond and Slansky conjectured that a new interaction similar to the strong interaction of the SM is able to confine, presumably at the TeV scale, all the unseen particles leaving at low energies only the SM families. This is known as the heavy color hypothesis.
Wilczek and Zee, showed that because of the large amount of families and mirror families the heavy color interaction is not asymptotically free and, thus, one cannot achieve a confining regime at the TeV scale [5]. This means that in a SO(18) theory one should observe 8 families and 8 mirror families below the electroweak scale, clearly against the experimental results.
A couple of years later, J. Bagger and S. Dimopoulos showed that a generalized Higgs mechanism cannot give us, as a final result, three chiral families at low energies 6. Their result was, that by using a Higgs mechanism, one should observe 4 families and 4 mirror families below the electroweak scale, making the other families and mirror families very heavy. However this is clearly not the case of the SM.
The SO(18) theory, as a unified theory of forces and families, had a short life. Because of the discouraging results by Wilczek and Zee and, independently by Bagger and Dimopoulos people stopped working on family unification theories. And the dream of a Unified Theory of forces and matter faded away.
References
- H. Georgi and S. Glashow, Phys.Rev.Lett. 32, 438 (1974). ↩
- H. Fritzsch and P. Minkowski, Ann. Phys. 93, 193 (1975). ↩
- M. Gell-Mann, P. Ramond, and R. Slansky, Conf. Proc. C790927, 315 (1979), 1306.4669. ↩
- Y. Fujimoto, Phys. Rev. D, Vol. 26, No. 11 (1982) 3183-3194. ↩
- F. Wilczek and A. Zee, Phys. Rev. D25, 553 (1982). ↩
- J. Bagger and S. Dimopoulos, Nucl. Phys. B244, 247 (1984). ↩
1 comment
Great summary even I am able to understand. Thanks!