Family unification (2): The SO(18) spinor strikes back

In the previous post, Family unification 1, we reviewed the historical development of Grand Unified Theories (GUT) of force and matter, i.e. Comprehensive Unification. We saw how the SO(18) spinor, 256, is able to accomodate the Standard Model (SM) family structure, however it contains too many families and, also, phenomenologically dangerous mirror families. During the 80’s it was thought that nothing could escape this threatening landscape, the SO(18) theory was thought to be doomed. A new article ¹ suggests this theory might not be dead.

Let’s think about this one more time. What makes the SO(18) theory to fail? If one goes slowly along the problem, it is easy to see that the root of the problem is chirality. When the 256 spinorbreaks down it contains families with SM quantum numbers for both chiralities, left and right. However, as it is well known, the weak interaction is left-handed. Going deeper, chirality arises as a space-time property. In fact, chirality can only be defined in a space with an even number of dimensions (more concretely, chirality is associated to SO(2N) algebra). What happens if we extend our space-time?

Extra-dimensional theories have been widely studied, both in the context of string theory ² and also in more bottom-up approaches ³. We don’t have to go to very high dimensional space-times to appreciate some interesting properties. In fact, a solution to the chirality problem can be found in a 5-dimensional space: chirality only exist in spaces with even number of dimensions and, thus, 5-dimensional fermions are not chiral. This, as we will see, is deeply related with family unification.

Our visible world, however, is clearly 4-dimensional. One way to overcome this obvious difficulty is to compactify the extra dimension. Moreover, it can be shown that by compactifying the extra dimension in a non-trivial way one can “select” which chirality, for any fermion, will appear at low energies ⁴. In other words, the 5-dimensional world is non-chiral but we can obtain a chiral 4-dimensional theory from it. At the same time, when a gauge theory is defined in the 5-dimensional world, the compactification mechanism can be used to reduce the initial symmetry in a kind of symmetry breaking mechanism. This mechanism is known as orbifold compactification and it is widely used to obtain 4-dimensional theories from higher dimensional theories and, also, to break gauge symmetries by using the non-trivial topology of the orbifold.

Let’s come back to Comprehensive Unification. Our starting point is a SO(18) gauge theory in a 5-dimensional anti-de Sitter space, AdS₅, also known as Randall-Sundrum space-time. In addition we compactify the extra dimension in an orbifold S₁/(Z₂xZ₂). In this particular space, the extra dimension is not flat but warped. It is described by the metric:

Thanks to the orbifold symmetry breaking mechanism we reduce the initial SO(18) gauge symmetry down to SO(10)xSO(8). This will be the gauge symmetry that is observed at the 4-dimensional effective theory. The same mechanism, that is orbifold compactification, that triggers gauge symmetry breaking is able to “select” only one chirality for the fermionic modes, this is the main point of our theory. In particular, after compactification, the 256 spinor splits as:

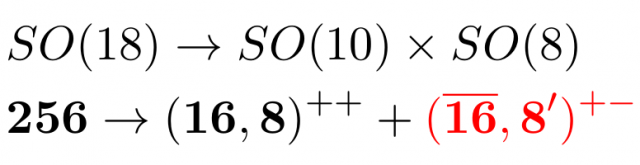
where the (+,+) or (+,-) refer to the boundary conditions on the UV and IR brane, respectively. From the 4-dimensional point of view, only fields with (+ +) boundary conditions have a massless excitations, i.e., massless quantum fields. The right handed mirror families (in red color) become heavy Kaluza-Klein modes and disappear from the low energy spectrum of the theory.

At this point, we have a 4-dimensional Grand Unified theory. To obtain the SM one has to implement a standard Higgs mechanism. Our theory consist on a GUT with 8 families, related by the SO(8) symmetry. Despite the situation does not seem better than in the pioneer papers of the 80s ⁵⁶⁷⁸, one has to carefully analyze the situation. After the orbifold symmetry breaking, only left-handed families will be present at low energies, and performing the appropiate calculations one observes that the heavy color hypothesis (see the previous post Family Unification 1) can be properly realized. The reason is that without the mirror families the hypercolor interaction (green line in figure 1) is asymptotically free, being strongly coupled and confining at low energies. This is one of the main results of the new framework.

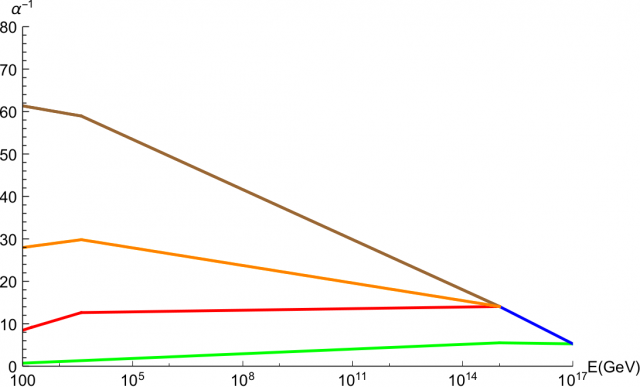
The upshot is that, at low energies, we have 3 families and 5 hypercolored families. This extra hypercolored families will be confined forming a new form of matter, hyperbaryons. Although they are highly stable individually, hyperbaryons can annihilate into ordinary matter in pairs. Conversely, they might be pair-produced in high energy collisions.

Thus for masses below 10 TeV the relic hyperbaryons contribute only a small fraction of the mass density of the universe. In consequence, though the current hyperbaryon relic abundance presents no obvious phenomenological catastrophe, the relic hyperbaryons might conceivably be detectable. One may also envisage that the lightest hyperbaryon might contribute to the dark matter density, as suggested in ⁹. It is noteworthy that this cosmological mass bound ensures that if they exist at all, hyperbaryons are not far beyond the reach of high-energy accelerators currently under discussion.

Far from being a fully realistic theory, the new article suggests that the idea of Comprehensive Unification should not be forgotten. The new framework, based in a 5 dimensional space-time, employs some mechanisms that were not completely developed when the SO(18) theory was first proposed. More research has to be done in this direction to explore the potential of Comprehensive Unification. Future experiments will tell us whether Nature can be described with this theory or not.