What the heck is a phonon?
We tacitly assume that perfect order exists throughout crystalline materials on an atomic scale when we discuss crystals in general. However, such an idealized solid does not exist at all in nature. All of them contain large numbers of various defects or imperfections. As a matter of fact, many of the properties of materials are profoundly sensitive to deviations from crystalline perfection; the influence is not always adverse, and often specific characteristics are deliberately fashioned by the introduction of controlled amounts or numbers of particular defects.
Let’s call crystalline defect to any lattice irregularity having one or more of its dimensions on the order of an atomic diameter. Think about it for a moment. This definition is about to bring a surprising result.
A first consequence is that we can classify crystalline imperfections according to the geometry or dimensionality of the defect. Some of these crystalline defects are point defects (those associated with one or two atomic positions), linear (or one-dimensional) defects, and interfacial defects, or boundaries, which are two-dimensional. Impurities may exist as point defects.
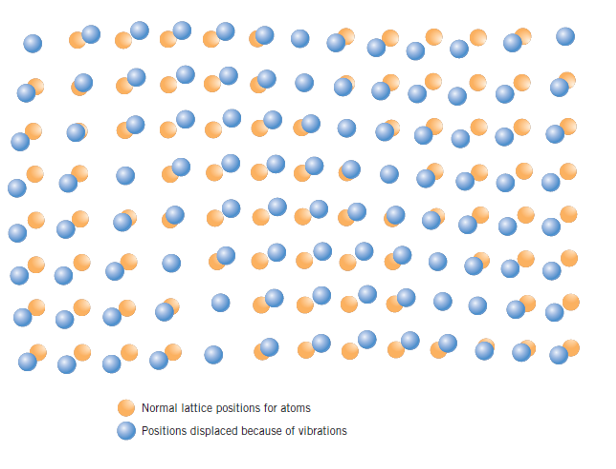
Consider this now. Every atom in a solid material is vibrating very rapidly about its lattice position within the crystal. In a sense, these atomic vibrations may be thought of as imperfections or defects. Why not? They suit the definition! Nobody said the irregularity was a permanent one!
Thus, atoms vibrate. But, at any instant of time not all atoms in a crystal vibrate at the same frequency and amplitude, nor with the same energy. Over time the vibrational energy of any specific atom will also vary in a random manner. It follows that at a given temperature there will exist a distribution of energies for the constituent atoms about an average energy. With rising temperature, this average energy increases, and, in fact, the temperature of a solid is really just a measure of the average vibrational activity of atoms and molecules.
Many properties and processes in solids are manifestations of this vibrational atomic motion, as is the case with any defect. In most solids the principal mode of thermal energy assimilation is by the increase in vibrational energy of the atoms. Again, atoms in solid materials are constantly vibrating at very high frequencies and with relatively small amplitudes. At room temperature, a typical vibrational frequency is on the order of 1013 vibrations per second, whereas the amplitude is a few thousandths of a nanometer. Melting, for example, occurs when the vibrations are vigorous enough to rupture large numbers of atomic bonds.
However, as we have just mentioned, atoms are bonded to other atoms in the crystal . Rather than being independent of one another, the vibrations of adjacent atoms are coupled by virtue of the atomic bonding. These vibrations are coordinated in such a way that travelling lattice waves are produced (see Figure 1).
Lattice waves may be thought of as elastic waves or simply sound waves, having short wavelengths and very high frequencies, which propagate through the crystal at the velocity of sound. The vibrational thermal energy for a material consists of a series of these elastic waves, which have a range of distributions and frequencies. The thermal scattering of free electrons during electronic conduction is by these vibrational waves, and these elastic waves also participate in the transport of energy during thermal conduction.
But, and this is an important point, we know that at the atomic scale quantum phenomena become apparent. Hence, only certain energy values are allowed. Einstein’s famous predictions for the behavior of the specific heat of solids as a function of temperature, for instance, were based on an application of the quantum hypothesis to a model of a crystalline solid in which the lattice atoms behave as three-dimensional oscillators vibrating with quantized energies.
So, we need a name for this minimum unit of energy. And, finally, here we are: A single quantum of vibrational energy is called a phonon.
Some final remarks:
Yes, a phonon is analogous to the quantum of electromagnetic radiation, the photon. As is the case with the photon, we may think of the phonon as actually being a particle, or we can think of the phonon as being a quantized wave.
Yes, it is true that, on occasion, the vibrational waves themselves are termed phonons.
Author: César Tomé López is a science writer and the editor of Mapping Ignorance.
References:
Callister & Rethwisch (2010) Materials Science and Engineering. An Introduction. 8th Edition. John Wiley & Sons Inc.
Steven H. Simon (2012) Lecture Notes for Solid State Physics (Hilary Term 2012). Oxford University
2 comments
It helps me a lot to completemy assignmen.
This real explains phonon very well for beginners. I learned from it, cheers!