Topology of disconnected elementary band representations

The revolutionary theory of topological quantum chemistry ¹, a description of the universal global properties of all possible band structures and materials, diagnoses topological phases based on elementary band representations. A set of bands is topological if it lacks an “atomic limit” that obeys the crystal symmetry (and time reversal, if desired): formally, an atomic limit exhibits a set of localized, symmetric Wannier functions, the counterpart of localized molecular orbitals for crystalline systems . This definition includes all known topological insulating phases.

It has been shown that each atomic limit defines a “band representation,” which is a representation of the full space group. The irreducible representations (irreps) of the little group at each point in the Brillouin zone are completely determined for each band representation. However, the little group irreps do not define the band representation: two groups of bands can exhibit the same little group irreps but differ by a Berry phase.

If a set of bands, separated by an energy gap from all other bands, does not transform as a band representation, it does not have localized, symmetric Wannier functions; consequently, it is topological .

An “elementary” band representation (EBR) is not equivalent to a sum of two band representations. It follows that a disconnected (gapped) elementary band representation must realize a set of topological bands. Such disconnected EBRs has been the focus² of a international team of researchers, including UPV-EHU, CFM and DIPC ones. All EBRs and their irreps at high-symmetry points in the Brillouin zone can be found on the Bilbao Crystallographic Server.

The theory of topological quantum chemistry also brings to light the different types of trivial-to-topological phase transitions, distinguished by how many symmetry-distinct orbitals contribute to the topological bands. For example, the Kane-Mele model of graphene requires only one type of symmetry-distinct orbital (the two spinful p_z orbitals per unit cell are related by the honeycomb lattice symmetry), while the trivial-to-topological transition in HgTe requires both s and p orbitals to create a “band inversion.” These two types of topological insulators differ in their atomic limit as the distance between atoms is taken to infinity: in the atomic limit of graphene, the band structure consists of a single flat and fourfold degenerate band, corresponding to a single EBR. In contrast, in HgTe, the atomic limit will consist of two flatbands, one each for the s and p orbitals, corresponding to two distinct EBRs.

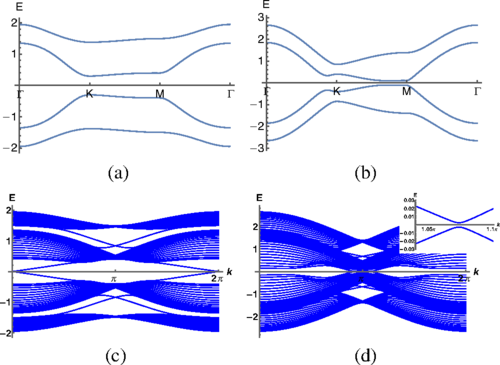
The team of researchers has focused on the graphene-like case: topological insulators that derive from a single orbital and its symmetry-related partners. In the language of band representations, the conduction and valence bands together transform as a single EBR; consequently, either the conduction or valence bands (or both) lack an atomic limit and are topological.

The researchers introduce models for a symmorphic and a nonsymmorphic space groups. A space group is called symmorphic (or split) if there is a point such that all symmetries are the product of a symmetry fixing this point and a translation.

The symmorphic example describes p_x,y orbitals on the honeycomb lattice. Without spin-orbit coupling, the band structure can be a (gapped) topological crystalline insulator. With infinitesimal spin-orbit coupling and time-reversal symmetry, the system exhibits a nontrivial ℤ₂ index.

The scientists are motivated to explore the nonsymmorphic example because, as part of their ground-breaking work on the connectivity of energy bands, Michel and Zak conjectured that spinless EBRs in nonsymmorphic space groups cannot realize a gapped band structure. This new results are a counterexample to Michel and Zak’s claim.

Thus, for each example, a topological invariant is constructed to explicitly demonstrate that the valence bands are nontrivial.. In doing so, they find a new topological invariant in a nonsymmorphic space group: a Dirac cone in the Wilson loop spectrum and a Wilson loop that winds along a bent path. As a plus, they also introduce the notion of a weak symmetry indicator.

Author: César Tomé López is a science writer and the editor of Mapping Ignorance.