An additional contribution to the spin Hall effect induced by an electric current

The interactions between moving charges and magnetic fields can be quite complicated; more if we consider the quantum effects. One example is the collection of Hall effects.

Imagine that we have a conductor or a semiconductor through which a current is flowing. Then we apply a strong transverse magnetic field. As a result, we can measure a potential difference at right angles to both the current and the field caused by the deflection of charge carriers by the field. This effect was described by Edwin Hall in 1879 and is the classical Hall effect. It introduces a coefficient, R_H, a constant characteristic of the material.

The effect is used to investigate the nature of charge carriers in metals and semiconductors, in the Hall probe for the measurement of magnetic fields, and in magnetically operated switching devices.

A quantum mechanical version of the Hall effect can be found at very low temperatures, in which the Hall coefficient R_H is quantized. And, depending on the values of the coefficient, there are two types of quantum Hall effect. The integer quantum Hall effect has R_H given as an integer with great precision. It can be used for precision measurements of constants such as e (the elementary charge) and h (Planck’s constant). In the fractional quantum Hall effect, R_H has fractional values. The integer quantum Hall effect can be understood in terms of non-interacting electrons, whereas the fractional effect is thought to result from many-electron interactions in two-dimensional systems.

Now we can use these charge-related Hall effects to try to understand their spin analogue (it is not, strictly speaking, a Hall effect).

The analogue of the Hall effect for spin, the spin Hall effect (SHE), is the accumulation of particles with opposite spin on the opposite surfaces of a material in which a current is flowing. However, the analogy is not complete since an external magnetic field destroys the effect. The SHE is due to spin-orbit coupling and this coupling can be intrinsic or extrinsic to the material: the intrinsic mechanism would be a consequence of the band structure of the material, whereas the extrinsic mechanism would stem from scattering of the charge carriers by impurities that locally induce spin-orbit coupling.

In the anomalous version of the quantum Hall effect, the anomaly is that a finite Hall voltage is present even in the absence of an external magnetic field. The quantum anomalous Hall state is characterized by a dissipationless edge mode carrying electrons of only one spin direction.

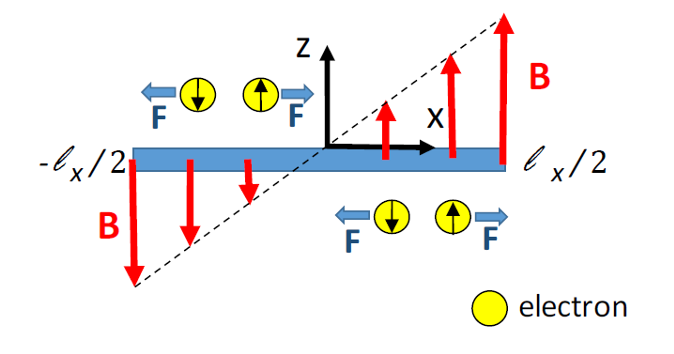
Now, a team of researchers analyzes ¹ an additional contribution to the SHE, arising from the existence of non-homogeneous magnetic fields within the metallic sheet.

The spin accumulation at the edges arises from the Zeeman coupling to the in-homogeneous magnetic field which exists within the sample. The gradient of the Zeeman coupling acts like a force which accelerates the carriers in the direction perpendicular to the current, in opposite way for spin up and spin down electrons, where the spins are oriented along the magnetic field. As a result, a gradient in the spin density within the sample is induced and spin imbalances appear which are comparable to those derived from the extrinsic and intrinsic mechanisms mentioned earlier.

The analysis does not rely explicitly on the existence of a strong spin orbit coupling, so that it can be generalized to metals made from light elements. The effect is found to be relativistic in nature, and its contribution to the spin Hall angle depends on the value of the velocity of light. Nothing strange as the Zeeman energy can be considered a relativistic effect which arises directly from the Dirac equation describing electrons.

Author: César Tomé López is a science writer and the editor of Mapping Ignorance

Disclaimer: Parts of this article are copied verbatim or almost verbatim from the referenced research paper.