An efficient tensor network algorithm for capturing thermal states of 2D quantum lattice systems
The concept of vector should be familiar: a quantity for which both magnitude and direction must be stated. This compares with a scalar quantity, where direction is not applicable, like temperature in a precise point. But, what if the magnitude varies with the direction? A vector would be a particular case, with only one direction, but it is possible to think of quantities that have different values for different directions. Welcome to the world of tensors.
Tensors are a mathematical concept that encapsulates and generalizes the idea of multilinear maps, i.e. functions of multiple parameters that are linear with respect to every parameter 1.You may have heard about tensors in connection to general relativity where they are used to describe spacetime. But tensors have also found their way into the realm of quantum many-body problems through tensor networks. A tensor network is simply a countable collection of tensors connected by contractions.
There is now a lot of excitement about tensor network algorithms based on the fact that certain classes of quantum systems can now be simulated more efficiently. These methods approximate a complicated quantum state using a tensor network with a simplistic, regular structure essentially applying lossy data compression that preserves the most important properties of the quantum state.
The study of two-dimensional strongly correlated systems with tensor network methods, however, comes with serious numerical effort and conceptual challenges. For example, projected entangled pair states (PEPS), which generalize matrix product states to higher dimensions, allows to grasp pure ground states of two-dimensional models. For thermal states, though, the numerical challenge is even harder, where only a few methods have been proposed for simple spin systems in sharp contrast to ground state calculations. Since two-dimensional quantum systems at finite temperature are ubiquitous in a number of contexts, like quantum materials in real laboratory conditions or systems of ultracold atoms in optical lattices in instances of quantum simulations, this lack of workable methods is a serious problem.
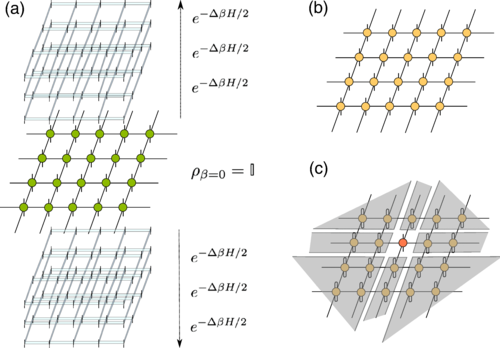
Now, an international team that includes Ikerbasque Research Professor Román Orús (DIPC) has developed an efficient tensor network algorithm for capturing thermal states of quantum lattice systems in two spatial dimensions and in the thermodynamic limit.
The new approach 2 develops a previous concept by Orús and others 3. The scheme starts from an infinite-temperature state and simulates the cooling down towards lower temperatures until reaching the desired regime. It uses the vectorization of a PEPS together with simple update and corner transfer matrix techniques.
The authors benchmarked the algorithm with the exact solution of the 2D Ising model on the square lattice, and applied it subsequently to study finite-temperature properties of the Bose-Hubbard model on the square lattice. While the Ising model is an excellent benchmark , the study of the Bose-Hubbard model allows the comparison with realistic lab settings in optical lattice experiments performing quantum simulations of strongly correlated matter. The new method demonstrated that it is fast and easy to implement, whenever PEPS expertise is available for ground state calculations.
This new approach will become a versatile tool in future studies of finite-temperature properties of two-dimensional quantum matter, and in the benchmarking of optical-lattice experiments in two dimensions under real-life laboratory conditions.
Author: César Tomé López is a science writer and the editor of Mapping Ignorance
Disclaimer: Parts of this article are copied verbatim or almost verbatim from the referenced research paper.
References
- Jacob Biamonte & Ville Bergholm (2017) Quantum Tensor Networks in a Nutshell arXiv:1708.00006 (quant-ph) ↩
- A. Kshetrimayum, M. Rizzi, J. Eisert, and R. Orús (2019) Tensor Network Annealing Algorithm for Two-Dimensional Thermal States Phys Rev. Lett doi: 10.1103/PhysRevLett.122.070502 ↩
- A. Kshetrimayum, H. Weimer, and R. Orús, Nat. Commun. 8, 1291 (2017). ↩