Tensor networks everywhere

Originally developed in the context of condensed-matter physics and based on renormalization group ideas, tensor networks have been revived thanks to quantum information theory and the progress in understanding the role of entanglement in quantum many-body systems. Ikerbasque Research Professor Román Orús, one of the world foremost authorities in the field, has just published 1 in Nature Reviews Physics an overview of the basic concepts and key developments in tensor networks applications to a variety of scientific disciplines.
The concept of vector should be familiar: a quantity for which both magnitude and direction must be stated. This compares with a scalar quantity, where direction is not applicable, like temperature in a precise point. But, what if the magnitude varies with the direction? A vector would be a particular case, with only one direction, but it is possible to think of quantities that have different values for different directions. Welcome to the world of tensors.
You may have heard about tensors in connection to general relativity where they are used to describe spacetime. But tensors have also found their way into the realm of quantum many-body problems through tensor networks. Tensor networks (TN) are mathematical representations of quantum many-body states based on their entanglement structure.
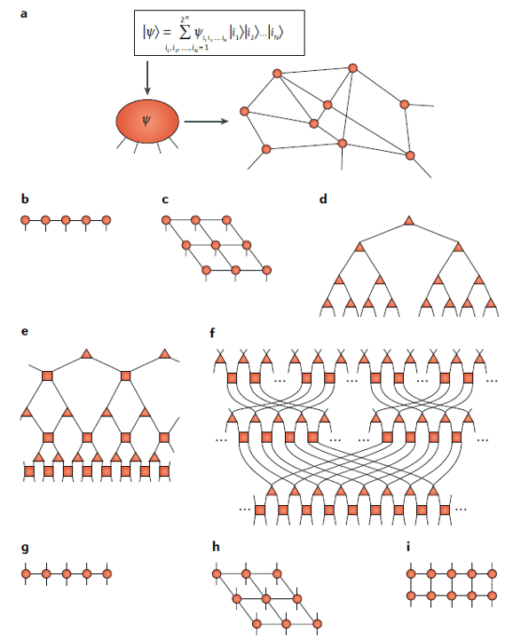
tensor networks.
The field started with a variational approximation for the 2D classical Ising model that is considered to be a precursor of TN variational methods. But it was not until the 1990s that researchers started to investigate more seriously how the TN structures arising from classical partition functions were intimately linked to the wavefunctions of quantum lattice systems. While trying to remove degrees of freedom that are not relevant to describe a complex system at different scales of some physical variable (renormalization) in the matrix that appears when you treat the system and its electron wave functions in linear-algebraic terms (density matrix), a key development was introduced: the density matrix renormalization group (DMRG). It turned out that the relevant degrees of freedom kept after renormalization were entanglement degrees of freedom of the wavefunction. DMRG was extremely successful, and it quickly became the tool of reference for 1D quantum lattice systems at low energies.
In the 2000s, physicists working on quantum information came to understand that entanglement has an inner structure that can be described by TNs. From there on, developments in TN methods continued mostly at the crossover between condensed matter physics and quantum information. TNs are also relevant to other scientific areas such as quantum gravity, for example, through the anti-de Sitter/conformal field theory correspondence (AdS/CFT), or artificial intelligence, in which it has been proven that neural networks have a TN structure.
It is thus worth keeping in mind that, in such crossover applications (for example, to artificial intelligence), the typical properties of quantum mechanics, such as unitarity, are lost. In such situations, the TNs no longer encode an entanglement structure of a complex system, but rather the structure of its generalized correlations, quantum or not.
The applications of TNs go well beyond quantum science. TNs are likely to continue finding numerical and theoretical applications, both along established research directions and new ones. The lesson we have learned over the years is that, essentially, anywhere there is a structure of correlations, there is also a TN, as they arise naturally whenever one has a tensor product structure. This means that there is room to apply our knowledge of quantum many-body entanglement. And sometimes this leads to unexpected connections and pleasant surprises, pushing forward the boundaries of science.
Author: César Tomé López is a science writer and the editor of Mapping Ignorance
Disclaimer: Parts of this article may have been copied verbatim or almost verbatim from the referenced research paper.
References
- Román Orús (2019) Tensor networks for complex quantum systems Nature Reviews Physics doi:10.1038/s42254-019-0086-7 ↩