Introducing fine-grained tensor network methods

The concept of vector should be familiar: a quantity for which both magnitude and direction must be stated. This compares with a scalar quantity, where direction is not applicable, like temperature in a precise point. But, what if the magnitude varies with the direction? A vector would be a particular case, with only one direction, but it is possible to think of quantities that have different values for different directions. Welcome to the world of tensors.

You may have heard about tensors in connection to general relativity where they are used to describing spacetime. But tensors have also found their way into the realm of quantum many-body problems through tensor networks. Tensor networks (TN) are mathematical objects which use the knowledge about the amount and structure of entanglement in quantum many-body states in order to reproduce the state accordingly. TN states also show up in other disciplines, such as quantum gravity, artificial intelligence, and even linguistics.

During the past decade there has been a rapid development of tensor network states and numerical methods for simulating strongly correlated quantum many-body systems. These TN methods use Ansätze – educated guesses or additional assumptions made to help solve a problem, and which is later verified to be part of the solution by its results – with remarkable success to simulate quantum lattice systems in different regimes.

Despite being extremely versatile, TNs are not free from limitations, though. The most obvious one is the ability to capture the expected structure of entanglement in the TN Ansatz, i.e., to incorporate the correct scaling of the entanglement entropy. Too much entanglement in the quantum state is a limitation itself.

On top of these limitations, geometric bottlenecks are an additional problem to deal with. A similar one arises for higher-dimensional systems, where high-connectivity lattices are quite usual. This is a serious issue, since such large-connectivity lattices are usually linked to exotic phases of matter such as quantum-spin liquids. In both cases handling tensors with so many indices quickly becomes computationally expensive for numerical simulations.

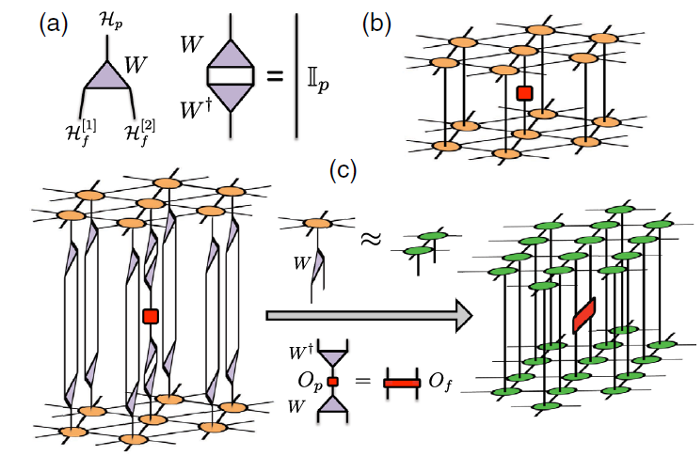
Now, a team of researchers proposes ¹ a physically motivated strategy to solve this problem in a efficient and accurate way. The idea is to break down the physical degrees of freedom into “smaller” pieces, i.e., to fine-grain the lattice. This can be done at the expense of introducing a set of fine-graining isometries. Under suitable conditions, then, this fine-graining simplifies the lattice and essentially keeps locality of interactions.

In other words, unlike other proposals of TN methods for high-connectivity lattices, this new approach preserves the correct geometric structure of the system, being better suited in terms of the entanglement structure. The key advantage being that the fine-grained lattice is easily amenable to TN methods.

The simulation of a triangular lattice with projected entangled pair states, for example, would naively imply tensors with six bond indices, if we were to use one tensor per lattice site. Handling tensors with so many indices quickly becomes a computational nightmare. The researchers use the fine-grain approach to compute ground-state properties of some models of the triangular lattice and benchmark the results against those obtained with perturbative continuous unitary transformations and graph projected entangled pair states, showing excellent agreement and also improved performance in several regimes.

This new approach will allow overcoming the computational cost associated to simulating lattices of high connectivity, such as the ones typically found for higher dimensional systems and frustrated quantum antiferromagnets and will become an instrumental tool in the discovery of new exotic phases of quantum matter.

Author: César Tomé López is a science writer and the editor of Mapping Ignorance

Disclaimer: Parts of this article may be copied verbatim or almost verbatim from the referenced research paper.