Quantum simulations of lattice gauge theories

A gauge theory is any number of quantum field theories put forward to explain fundamental interactions. In these theories the interactions between particles can be explained by the exchange of particles such as gluons, photons, and W and Z bosons. A gauge theory involves a symmetry group for the fields and potentials (the gauge group).

In the case of electrodynamics, the group is commutative, whereas the gauge theories for the strong and weak interactions use non-commutative groups. This difference explains why quantum electrodynamics is a much simpler theory than quantum chromodynamics, which describes the strong interaction, and electroweak theory, which is a unified theory of the weak and electromagnetic interactions. The gauge group is even more complex for gravity.

Gauge theories also appear in condensed-matter physics in the description of emergent phenomena, where the ℤ₂ lattice gauge theory arises as an effective model for high temperature superconductors; and in quantum information, where some quantum error-correcting codes are deeply related to lattice gauge theories. Even if gauge theories are widely used in modern physics, most of them can not be solved exactly, and one has to resort to either perturbative expansions or numerical methods to extract quantitative predictions, especially in the case of non-Abelian local symmetries.

Quantum simulators are a promising tool for studying unexplored regimes of gauge theories that remain inaccessible to our current analytical and numerical analyses, such as the study of dynamics or effects with finite fermion densities. In the quest of being able to simulate the most complex gauge theories, such as quantum chromodynamics, it is interesting to develop quantum simulations for simpler models that can capture relevant features of the more complex ones while being more amenable to current noisy quantum devices.

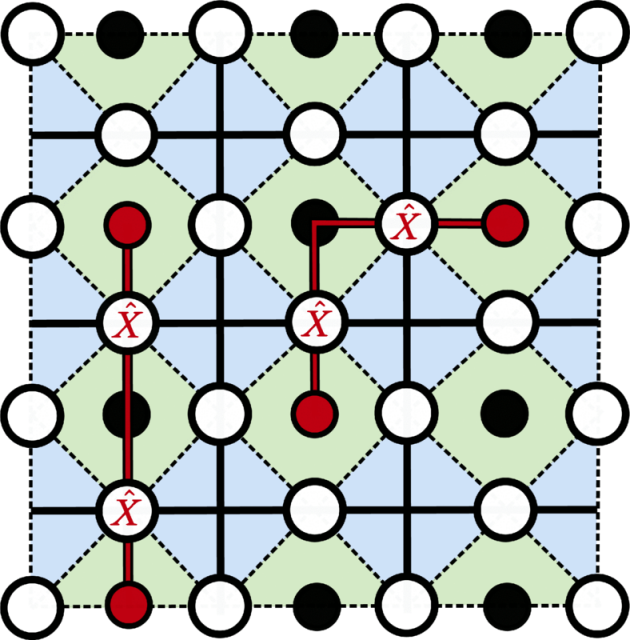
Now, a team of researchers proposes ¹ a dissipative variational quantum algorithm for studying ground-state properties of the ℤ₂ lattice gauge theory that outperforms previous unitary approaches both in the presence and absence of circuit-level noise.

The proposed algorithm consists of a variational ansatz wave function for the ground state of the ℤ₂ gauge theory containing a non-unitary operation together with a procedure for preparing it in quantum simulators. An ansatz is an educated guess made to help solve a problem, and which may later be verified to be part of the solution by its results

The researchers show that the proposed ansatz is a very good approximation to the real wave function by measuring physical properties that reveal exotic phenomena, such as the presence of confinement and a topological phase. They also prove that the new algorithm yields an advantage with respect to previous unitary ansatzes when the effect of the noise present in a real quantum simulator is considered.

The results presented in this work are a step toward quantum simulations of gauge theories and provide insights into the efficiency of variational algorithms in current noisy quantum devices.

Author: César Tomé López is a science writer and the editor of Mapping Ignorance

Disclaimer: Parts of this article may have been copied verbatim or almost verbatim from the referenced research paper/s.