Validity of the inhomogeneous Kibble-Zurek mechanism in the quantum domain
On 8 October 2013, following the discovery at CERN’s Large Hadron Collider of a new particle that appeared to be the long-sought Higgs boson predicted by the theory, it was announced that Peter Higgs and François Englert had been awarded the 2013 Nobel Prize in Physics. But they were the survivors of the bunch of people that predicted the mechanism back in 1964. And not the only ones, for Thomas Kibble was alive at the moment (he died in 2016). Actually Higgs himself always includes Kibble’s name when referring to what we know now as the Higgs mechanism, and Abdus Salam used to use the term Higgs-Kibble mechanism for the same.
But Thomas Kibble was not only famous for his involvement in the theoretical development of the Higgs mechanism. His research on phase transitions and topological defects is most significant. Actually, the Kibble-Zurek mechanism (KZM) is a paradigmatic theory to describe the dynamics across both classical continuous phase transitions and quantum phase transitions.
KZM describes the non-equilibrium dynamics and the formation of topological defects in a system which is driven through a continuous phase transition at finite rate. It is named after Kibble, who pioneered the study of domain structure formation in the early universe, and Wojciech H. Zurek, who related the number of defects it creates to the critical exponents of the transition and to how quickly the critical point is traversed.
The development of new methods to induce or mimic adiabatic dynamics – where time flows very slowly and the solution of the Schrödinger’s equation at one given time goes continuously over to the solution at another time – is essential to the progress of quantum technologies. In many-body systems, the need to develop new methods to approach adiabatic dynamics is underlined for their potential application to quantum simulation and adiabatic quantum computation.
But there is a problem. Usually, the system of interest is assumed to be driven by a quench of an external control parameter in a finite time across the critical value. KZM predicts that the average domain size exhibits a universal power-law scaling and that, at the boundary between domains, topological defects form. In other words, KZM constitutes a negative result for the purpose of suppressing defect formation, given that in an arbitrarily large system, defects will be formed no matter how slowly the phase transition is crossed.
The case that experimental reality is not ideal may be a solution. Test beds for the experimental demonstration of universal dynamics at criticality are often inhomogeneous, and it is this very feature which paves the way to defect suppression. Thus, under a finite-rate quench of an external control parameter, the system does not reach the critical point everywhere at once. Rather, a choice of the broken symmetry made locally at the critical front can influence the subsequent symmetry breaking across the system, diminishing the overall number of defects.
In this scenario, then, the paradigmatic KZM fails, and should be extended to account for the inhomogeneous character of the system. Hence, an inhomogeneous Kibble-Zurek mechanism (IKZM) has been formulated in classical phase transitions following the early insight by Kibble himself and Grigorii E.Volovik more than twenty years ago. Its key predictions are a suppression of the net number of excitations with respect to the homogeneous scenario, and an enhanced power-law scaling of the residual density of excitations as a function of the quench rate.
Now, Fernando J. Gómez-Ruiz and Ikerbasque Research Professor Adolfo del Campo (DIPC) 1 establish the universal character of the critical dynamics across an inhomogeneous quantum phase transition and the validity of the IKZM in the quantum domain.
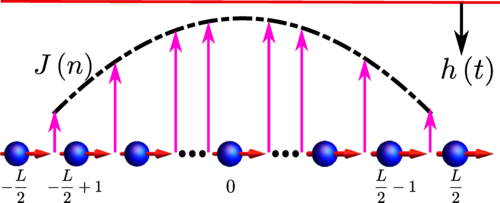
They show that, in inhomogeneous systems, as the critical point is reached locally, there is an interplay between the speed of sound and the velocity of propagation of the critical front. The effective system size in which topological defects can form acquires then a dependence on the quench rate. For fast quenches, the residual density of defects is well described by a power law in agreement with the original Kibble-Zurek mechanism. As the quench rate decreases there exists a crossover to a novel power-law scaling behaviour of the density of defects, which is characterized by a larger exponent, higher than that predicted by the Kibble-Zurek mechanism. In other words, local driving leads to a much more pronounced suppression of the density of defects. This is a testable prediction amenable to a variety of platforms for quantum simulation including cold atoms in optical lattices, trapped ions, and superconducting qubits.
These results should prove useful in a variety of contexts including the preparation of phases of matter in quantum simulators and the engineering of inhomogeneous schedules in quantum annealing.
Author: César Tomé López is a science writer and the editor of Mapping Ignorance.
References
- F. J. Gómez-Ruiz and A. del Campo (2019) Universal Dynamics of Inhomogeneous Quantum Phase Transitions: Suppressing Defect Formation Phys. Rev. Lett. doi: 10.1103/PhysRevLett.122.080604 ↩
2 comments
[…] Kibble-Zurek mekanismoak oker topologikoen sotze dinamika deskribatzen du. DIPCko ikertzaileek antzeman dute sistema ez homogeneoetan mekanismo hau aldatu behar dela eta horren ondorioz defektuak ia desagertu egiten direla. Hau oinarrizkoa da, esaterako, konputazio kuantikoan erabiliko diren materialentzat: Validity of […]
[…] El mecanismo de Kibble-Zurek describe la dinámica de formación de los defectos topológicos. La gente del DIPC ha descubierto que en los sistemas no homogéneos hay que alterar ese mecanismo y que, como consecuencia los defectos prácticamente desaparecen. Esto […]