A theory of spin hall magnetoresistance to study magnetism at interfaces

The interactions between moving charges and magnetic fields can be quite complicated; more if we consider the quantum effects. One example is the collection of Hall effects.

Imagine that we have a conductor or a semiconductor through which a current is flowing. Then we apply a strong transverse magnetic field. As a result, we can measure a potential difference at right angles to both the current and the field caused by the deflection of charge carriers by the field. This effect was described by Edwin Hall in 1879 and is the classical Hall effect. It introduces a coefficient, R_H, a constant characteristic of the material.

The effect is used to investigate the nature of charge carriers in metals and semiconductors, in the Hall probe for the measurement of magnetic fields, and in magnetically operated switching devices.

A quantum mechanical version of the Hall effect can be found at very low temperatures, in which the Hall coefficient R_H is quantized. And, depending on the values of the coefficient, there are two types of quantum Hall effect. The integer quantum Hall effect has R_H given as an integer with great precision. It can be used for precision measurements of constants such as e (the elementary charge) and h (Planck’s constant). In the fractional quantum Hall effect, R_H has fractional values. The integer quantum Hall effect can be understood in terms of noninteracting electrons, whereas the fractional effect is thought to result from many-electron interactions in two-dimensional systems.

Now we can use these charge-related Hall effects to try to understand their spin analogue (it is not, strictly speaking, a Hall effect).

The analogue of the Hall effect for spin, the spin Hall effect (SHE), is the accumulation of particles with opposite spin on the opposite surfaces of a material in which a current is flowing. However, the analogy is not complete since an external magnetic field destroys the effect. The SHE is due to spin-orbit coupling and this coupling can be intrinsic or extrinsic to the material: the intrinsic mechanism would be a consequence of the band structure of the material, whereas the extrinsic mechanism would stem from scattering of the charge carriers by impurities that locally induce spin-orbit coupling.

A manifestation of the SHE in a normal metal (NM) is a modulation of the magnetoresistance (MR) with respect to the direction of the applied magnetic field when the metal is in contact with a magnetic insulator (MI) in NM/MI structures.14–16 This effect, called the spin Hall magnetoresistance (SMR), has been observed in several experiments. The origin of the SMR is the spin-dependent scattering at the NM/MI interface which depends on the angle between the polarization of the spin Hall current and the magnetization of the MI. The latter can be controlled by magnetic fields.

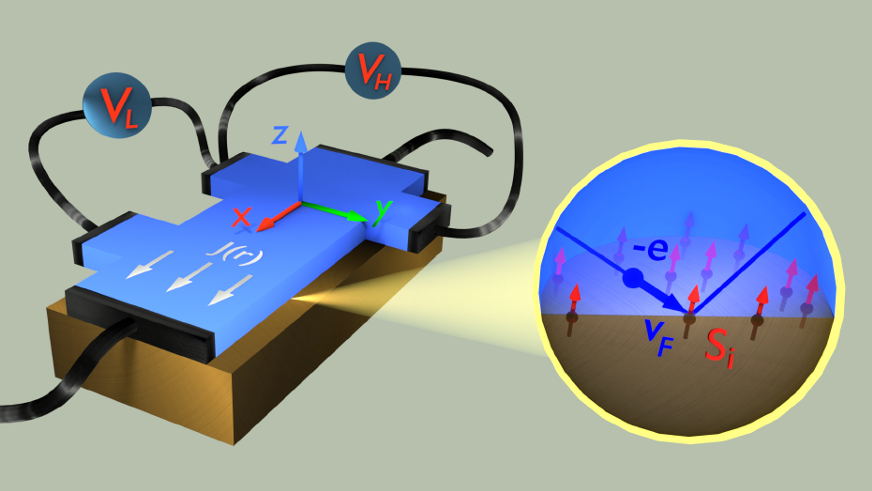
Although the theory of SMR is well established and provides a qualitative description of the effect, it does not describe the dependence of the resistivity on the strength of the applied magnetic field, nor on the temperature. Now, a team of researchers from DIPC, CFM and UPV/EHU ¹ presents a theory of the spin Hall magnetoresistance of metals in contact with magnetic insulators which describes that dependence.

Spin mixing conductances, which are at the heart of the SMR effect, have traditionally been regarded as phenomenological parameters in every experiment, because their computation was thought to be a formidable task which could only be carried out by ab initio methods. Recent experiments show, however, that the SMR effect depends both on the applied magnetic field and on the temperature, and that the magnetic state of the MI plays an important role for SMR. The authors have been able to express these conductances in terms of the microscopic parameters of the interface and the spin-spin correlation functions of the local moments on the surface of the magnetic insulator.

The researchers describe the spin-dependent scattering at the NM/MI interface via a microscopic model based on the sd coupling between local moments on the MI surface and itinerant electrons in the NM. The temperature and magnetic-field dependence of the interfacial scattering coefficients are obtained by expressing them in terms of spin-spin correlations functions. The latter are determined by the magnetic behavior of the MI layer.

As examples, the researchers study the MR of a metallic film adjacent to either a paramagnet (PM) or a Weiss ferromagnet (FM).

This new theory provides a useful tool for understanding the experiments on heavy metals in contact with magnetic insulators of different kinds, and it enables the spin Hall magnetoresistance effect to be used as a technique to study magnetism at interfaces.

Author: César Tomé López is a science writer and the editor of Mapping Ignorance

Disclaimer: Parts of this article may have been copied verbatim or almost verbatim from the referenced research paper.