Impurities and spin Hall effects in graphene
The interactions between moving charges and magnetic fields can be quite complicated; more if we consider the quantum effects. One example is the collection of Hall effects. There are analogues of these effects for spin and the detection of the most sophisticated one in graphene, where, at least, it should not be strong, is something to be explained.
Imagine that we have a conductor or a semiconductor through which a current is flowing. Then we apply a strong transverse magnetic field. As a result, we can measure a potential difference at right angles to both the current and the field caused by the deflection of charge carriers by the field. This effect was described by Edwin Hall in 1879 and is the classical Hall effect. It introduces a coefficient, RH, a constant characteristic of the material.
The effect is used to investigate the nature of charge carriers in metals and semiconductors, in the Hall probe for the measurement of magnetic fields, and in magnetically operated switching devices.
A quantum mechanical version of the Hall effect can be found at very low temperatures, in which the Hall coefficient RH is quantized. And, depending on the values of the coefficient, there are two types of quantum Hall effect. The integer quantum Hall effect has RH given as an integer with great precision. It can be used for precision measurements of constants such as e (the elementary charge) and h (Planck’s constant). In the fractional quantum Hall effect, RH has fractional values. The integer quantum Hall effect can be understood in terms of noninteracting electrons, whereas the fractional effect is thought to result from many-electron interactions in two-dimensional systems.
Now we can use these charge-related Hall effects to try to understand their spin analogue (it is not, strictly speaking, a Hall effect).
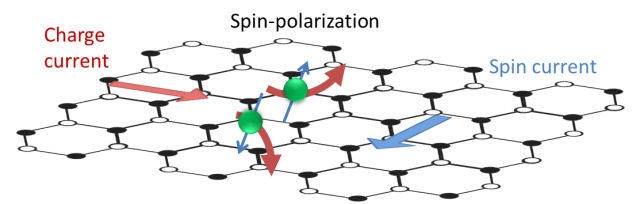
The analogue of the Hall effect for spin, the spin Hall effect, is the accumulation of particles with opposite spin on the opposite surfaces of a material in which a current is flowing. However, the analogy is not complete since an external magnetic field destroys the effect. The spin Hall effect is due to spin-orbit coupling (see [1] How to induce a giant spin-orbit effect in graphene for a detailed explanation) and this coupling can be intrinsic or extrinsic to the material: The intrinsic mechanism is a consequence of the band structure of the material, whereas the extrinsic mechanism stems from scattering of the charge carriers by impurities that locally induce spin-orbit coupling (see The spin texture of surfaces and electron scattering).
Now a team of researchers, that includes Miguel Ángel Cazalilla from DIPC, has investigated the effect of spin-orbit active impurities on the extrinsic spin hall effect in graphene. 1
Since spin-orbit coupling is a relativistic effect that is typically strongest in materials containing heavy atoms, the spin-orbit coupling in graphene is expected to be weak. Therefore, graphene has been suggested as an ideal material for passive spintronics, for which a long spin diffusion length is required, spin-orbit coupling in the material being a major limiting factor.
However, motivated by the search for materials exhibiting the quantum spin Hall effect, it has been theoretically predicted, and experimentally observed, that the spin-orbit coupling can be greatly enhanced in graphene by means of deposition of metal atoms. In the limit of a dilute number of impurities (i.e., adatoms), in which the excellent charge-carrier mobility properties of graphene are not strongly modified, heavy adatom clusters have been predicted to induce a sizable spin Hall effect.
On the other hand, studying spin-orbit couplings at surfaces is critical to understand electron scattering and the generation of spin currents. The so-called spin texture at the surface is characterized by the Rashba effect, a splitting of the spin-up and spin-down states in energy and momentum, and the effect of spin-orbit couplings at the surface can be qualitatively described by the Rashba-Bychkov model.
The researchers have focused on understanding the effects of Rashba anisotropy on the charge and especially spin transport properties, and, in particular, the spin Hall angle, which is a measure of the conversion efficiency between charge currents and pure spin currents, and it is a material dependent parameter.
Their model shows that anisotropy arises as a consequence of the arrangement of adatoms in the clusters decorating a single layer of graphene and that spin-orbit couplings are effectively generated when the arrangement lowers the symmetry of the system from the hexagonal symmetry of graphene. They find that Rashba anisotropy can strongly modify the dependence of the spin Hall angle on carrier concentration.
The model provides a simple and general description of the skew scattering mechanism due to the spin-orbit coupling that is induced by the proximity to large clusters of impurities in graphene.
Author: César Tomé López is a science writer and the editor of Mapping Ignorance.
References
- H.-Y. Yang, Chunli Huang, H. Ochoa, and M. A. Cazalilla (2016) Extrinsic spin Hall effect from anisotropic Rashba spin-orbit coupling in graphene Physical Review B DOI: 10.1103/PhysRevB.93.085418 ↩