Chirality can be used to control the sign of a maximal Chern number

The magnitude of many of the exotic phenomena predicted for topological semimetals is directly proportional to something called the Chern number. Given the importance of the Chern number magnitude for these phenomena, it is just natural to wonder whether there is an upper limit for it and whether there are real materials in which this limit can be reached. Now, we have some answers.

Some materials have special universal properties protected against perturbations. Such properties are theoretically described by topology, a branch of mathematics concerned with the properties of geometrical objects that are unchanged by continuous deformations. So-called topological insulators are electronic materials that have a bulk band gap like an ordinary insulator but have conducting states on their boundaries, i.e., edges or surfaces. The conducting surface is not what makes topological insulators unique, but the fact that this surface state is particularly robust, potentially due to some symmetry like time-reversal.

A topological invariant is a geometrical quantity that remains unchanged by continuous deformations. Topological invariants are mathematical have found widespread applications in physics, chemistry, and materials science. One of the best known topological invariants in condensed matter physics is the Chern number.

The definition of the Chern number is not exactly simple. It is one of those concepts in physics that you can express far more easily using mathematics than words. We need to start with a Berry phase. A Berry phase is a phase that can appear in the wave function for a quantum-mechanical system that depends on various parameters when parallel transport is performed in the so-called parameter space, the set of all possible combinations of values for all the different parameters. Now, the Berry curvature is the gauge field associated with the Berry phase. Then, the Chern number is the flux of Berry curvature through a closed two-dimensional surface.

All that said, we can keep in mind that the Chern number, an integer, characterizes the topology of filled bands in two-dimensional lattice systems. A band with a non-zero Chern number is topologically non-trivial. When the highest occupied band is non-trivial and completely filled, the state is called a topological insulator.

Or take Weyl semimetals. Weyl fermions can also be described as point-like two-band crossings of the quasiparticle dispersion. These crossings are topologically protected because they carry a topological “charge”. This charge has an integer value (±1), the Chern number, and it is the one that gives the electronic wave function a handedness. In other words, in Weyl semimetals, not just the crystal structure itself, but also the electronic wave functions can exhibit a chirality. Chern numbers, thus, characterize wave functions.

It has recently been predicted that in chiral crystals, which possess neither mirror nor inversion symmetries, more complex band crossings can be pinned at high-symmetry lines or points that feature larger Chern numbers, up to a maximal magnitude of 4. For linear band crossings in magnetic materials, the maximal Chern number is also 4. This number has not been “observed” experimentally, though.

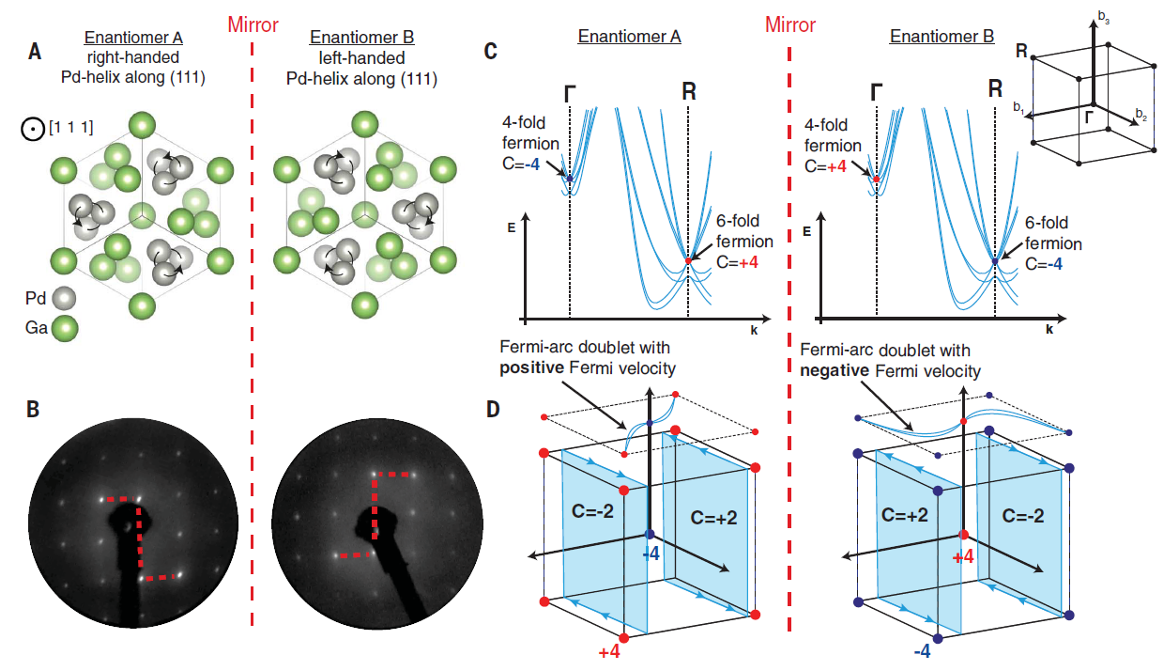
Now, a team of researchers has overcome ¹ the obstacles that prevented that experimental confirmation by investigating a different chiral topological semimetal candidate from those already tested: the intermetallic compound of palladium and gallium, PdGa. It belongs to space group 198, a family of chiral semimetals —including RhSi, CoSi, AlPt, and PdBiSb— which is expected to display a Chern number of magnitude 4.

PdGa has substantial spin-orbit coupling and can be prepared with flat, clean, and well-ordered surfaces by polishing and subsequent sputtering and annealing in ultrahigh vacuum. Using angle-resolved photoelectron spectroscopy (ARPES) and ab initio calculations, the researchers can clearly resolve the presence of multifold crossings in the bulk electronic structure of PdGa, as well as four topological Fermi arcs on its surface. This is equivalent to observing experimentally a Chern number of magnitude 4.

This result has a very interesting chemical consequence. PdGa is known as an important catalyst—for instance, for the semihydrogenation of acetylene—and shows potential for enantioselective catalytic reactions of chiral molecules. Because the Fermi arcs are mostly derived from d orbitals of Pd that are well known to be important for catalysis, they enlarge the reservoir of catalytically active charge carriers at the sample surface where chemical reactions take place. Additionally, the topological protection of nonzero Chern numbers could suppress passivation of the Fermi arcs, e.g., by hydrogenation.

PdGa crystals show a chiral motif in the shape of a helical arrangement of Pd and Ga atoms along the (111) direction. Therefore, two enantiomers of PdGa can be distinguished. The researchers grew both enantiopure specimens of PdGa and found a reversal of their Fermi-arc velocities, which demonstrates that the handedness of chiral crystals can be used to control the sign of their Chern numbers.

Author: César Tomé López is a science writer and the editor of Mapping Ignorance

Disclaimer: Parts of this article may be copied verbatim or almost verbatim from the referenced research paper.