A paradox in the thermodynamic arrow of time?

Let me make a short interruption in our series about the prehistory of philosophy of science, to discuss a completely different point. I am writing this now, just because in the last days I think I have been able to clearly formulate a specific perplexity that for many years I had felt about what we can call the ‘naive account’ of the THermodynamic Arrow of Time (THAT). It is not that I claim to have found a real ‘paradox’ or inconsistency in THAT, but simply that now I think I can make it explicit what I felt I didn’t understand in it, and I just want to invite readers to point to the fundamental elements of THAT (surely in its sophisticate, rather than its naive account) that I may very probably be missing and that are causing my (too probable) misunderstanding.

The thermodynamic arrow of time, in its naive exposition (which, not being a physicist, is the only one I think I grasp), is a putative ‘solution’ to the puzzling enigma of why it is that the world is so clearly time-asymmetric (i.e., for most phenomena it seems self-evident if one video recording of them is being projected ‘forward’ or ‘backwards’), in spite of the most fundamental laws of physics, either classical, relativistic or quantum-mechanical, being totally time-symmetric (i.e., if the progression of a physical system along the time dimension obeys those laws, the exact reversal of that progression also obeys the same laws). According to Ludwig Boltzmann’s statistical mechanics, the enigma would be solved by pointing to the fact that, in any thermodynamic system, there are much more possible states of high entropy than those of low entropy, and hence, it would be a matter of sheer probability that a system ‘left to itself’ will tend to occupy states of higher and higher entropy (or ‘disorder’). The time-asymmetry we observe in macroscopic phenomena would, hence, be an effect of the evolution of the universe tending statistically towards disorder (and this is what I am calling the naive account of THAT).

The paradox my title refers to consists in a particular difficulty I find in this explanation. In order to formulate it with the maximum clarity, it will be useful to introduce a few precise definitions. Let a, b, c… represent the possible states of a thermodynamically isolated system (that may coincide with the whole universe), each consisting in particles (or whatever ‘ultimate’ elements our preferred physical theory chooses) having a particular set of properties in each state (in classical physics, their positions and momentums –or mass multiplied by instantaneous velocity vectors–, as well as electric charges), and let U be the set of all those possible states. Now, to each single state we can associate two different subsets of U: first, S(a) will be the set of states that are macroscopically indistinguishable from a. States of high entropy are just those for which S(a) is very large, and viceversa. If a, b, c… represent ‘microscopic’ states, S(a), S(b), S(c)… represent ‘macroscopic’ states, in the sense that, even if a and b are different ‘in themselves’ (e.g., they have different particles placed in different locations, or moving in a different way…), it is the case that we cannot notice any difference between S(a) and S(b) (but perhaps we can distinguish both from S(c)).

Second, each state a belongs into the set H(a) that corresponds to those states from which it ‘comes’, and those that ‘come’ from it. I.e., to each state a we can associate its time line, or its history: the states through which a system has passed, thanks to its obeying the fundamental laws of physics. If the laws are deterministic, these lines are proper lines, in the sense that they do not ‘branch’, but this is actually irrelevant for my argument. Hence, the H’s represent the temporal evolution of the systems according to the physical laws. Figure 1 depicts several states S, and a temporal line H ‘flowing’ from one single microstate a. As it is clear from the image, the odds are in favour of H passing towards bigger and bigger S’s, as the naive THAT claims.

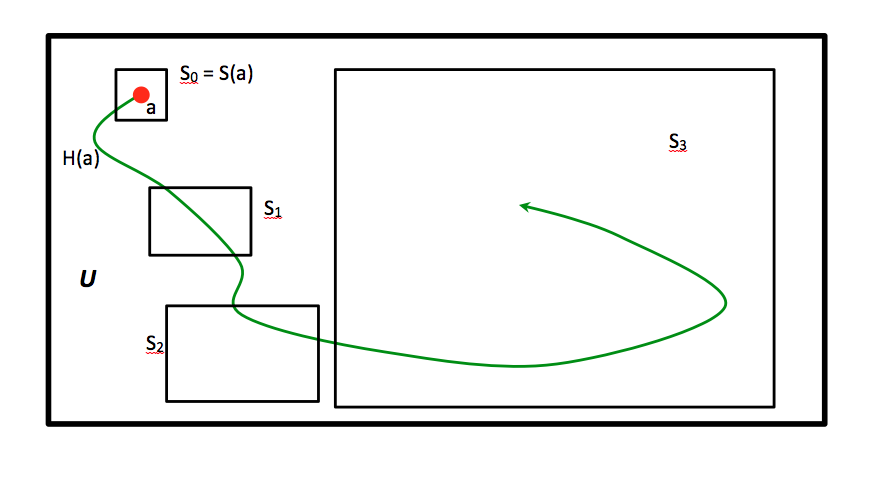
But here myfirst perplexityarises. For imagine a system b which is exactly equal to a, only that the velocity vectors of its particles point exactly 180º in the contrary direction. If we construct the future temporal line for b, H(b), the same ‘argument’ that has traditionally being employed to assert that “the odds are immensely in favour of H(a) evolving towards bigger and bigger, more and more entropic macrostates, just because most of U is covered by these”, wouldn’t it force us to assert that the evolution of system b will also tend to pass through bigger and bigger macrostates? Instead, and pretty obviously, what we can expect to really happen is that, since b is the exact reversal of a, its future evolution will be towards those states from which a ‘came’ in the past, i.e., states with lower and lower entropy, as in fig. 2 (I have assumed that S(a) = S(b), i.e., that both states are ‘macroscopically indistinguishable’, but this is not relevant for my argument).

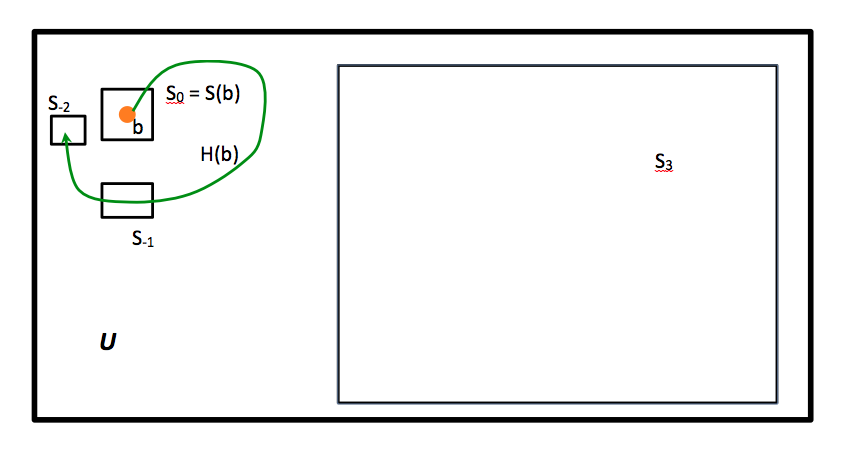
Arithmetic plays against the plausibility of the naive THAT in again one more way, because for every microscopic system we happen to choose, there is another system that is in the same relation to it as b is to a, and hence, the probability of choosing at random a time line H (a possible ‘history of the universe’, say) that ‘goes towards bigger and bigger entropy’ is exactly the same as the probability of choosing another timeline H’ that runs in the opposite direction. And hence, statistical mechanics would not explain why time flows in the direction it does (though perhaps it would explain why the flow is time-asymmetric anyway, something I will immediately show it is also not so evident). I think someone might be tempted to argue that the ‘real’ time direction is irrelevant, according to some reasoning like this one:

H’s would tend to pass through bigger and bigger macrostates, either in one time direction or in the other, and we simply call ‘future’ the direction in which entropy tends to grow. Perhaps there are universes, or there have been epochs in our own universe, in which the temporal evolution of molecular systems has led to states of lower and lower entropy and increasing order, but the inhabitants of those worlds would have, nevertheless, the impression of their time flowing towards the more disordered states. After all, since a and b are exactly specular to each other, their inhabitants would have exactly the same ‘memories’, i.e., they will ‘remember’ (both in a and b) having passed through S_-1 and S_-2, and not through S₁ and S₂.

But here comes my second perplexity: what we should expect from the naive view of THAT, as depicted in fig. 3, is that history world-lines, our H’s, are almost always time symmetric, in the sense that they spend most of the time in regions corresponding to high entropy states, and also in the sense that they show exactly this same tendency in both temporal directions. This is shown in fig. 3, where a time line H(a) passing through a has been divided in a ‘future’ (darker) and a ‘past’ (lighter) segments, both of which tend to go to states more entropic than S(a). Lines like this new H(a) would represent the ‘statistically normal’ thermodynamic evolution of a molecular isolated system: one in which the system ‘falls’ sometimes in low-entropy states, but soon goes out of them, and where this ‘fallings’ occur with equal probability towards the past and towards the future. Stated otherwise: randomly picking any point in the history of the universe, or of any isolated thermodynamic system, it should be the case (statistically speaking) that time seems to flow ‘towards the future’ starting from that point, both if we follow the evolution of the system towards the real future, and if we follow its evolution towards its real past.

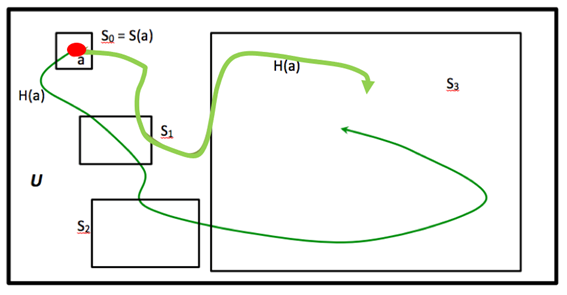
In a sense, what archaeology, palaeontology and cosmology should show us, if the naive view of THAT were correct, would be that, in the past, things got more and more disordered, that (let’s say) dinosaurs walked backwards, ‘grew smaller’, and got into their eggs by the end of their lives. What view of THAT does not explain, to say it otherwise, is why the past looks like a past, and not like a future. Of course, it is not that a universe like ours is mathematically incompatible with statistical mechanics; far from that. My point is, simply, that a universe that has been so stubbornly time-asymmetric in all the billion years of its history, seems to be a pretty weird one from the point of view of that theory.

But, I insist, I am only a science aficionado, and so it’s almost certain that I am missing some elements in the sophisticate picture of THAT, that can make my ‘paradox’ or ‘perplexities’ to vanish. It would be great, then, if anybody could provide our readers with a sufficiently understandable summary of that sophisticate account, one that explains why a ‘stubborn asymmetric flow of time’ is what we can expect from the laws of physics.