The Hubble tension in perspective: A crisis in modern cosmology?
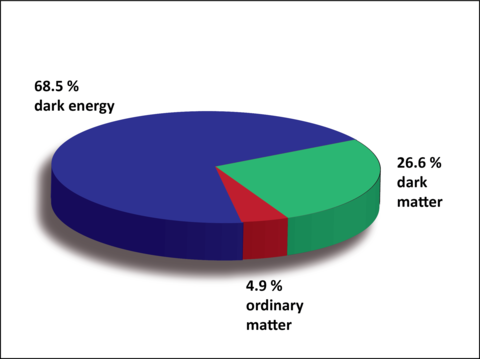
Imagine a Universe that started with a huge explosion setting the beginning of space and time to the point that such concepts have no meaning until then. Imagine a Universe that, after an inflationary phase (extremely fast expansion), kept expanding and forming stars and galaxies distributed in a sponge-like structure dominated by walls and filaments and huge voids completely depleted of matter. In such Universe, around two thirds of its energy and matter is dark energy (accelerating this expansion), nearly 25% is dark matter that cannot be seen and moves only slowly, and the rest, only 5%, is ordinary matter (see figure 1). This, dear reader, is the Universe we live in, at least according to the current paradigm, the Λ-Cold Dark Matter model (ΛCDM).
ΛCDM is one of the most polished theories in science. It explains a great number of observations and has outlived many challenges. However, we should highlight the complexity behind it. Let’s remember that Astronomy is an observational science. We can crunch numbers, we can think of theories and hypothesize as we wish, but there is no way of developing a cosmological laboratory. Thus, we need to observe the surrounding cosmos in order to do Astronomy. One of the basic concepts that make observational cosmology possible is the fact that the speed of light is finite, meaning that more distant objects reveal properties at earlier times in the history of the Universe. However, we cannot measure distance nor time in the Universe! We only observe what we call “redshift”, the apparent change in wavelength of absorption and emission lines in spectra (a consequence of the cosmological Doppler effect: the fastest an object is receding from us or approaching to us, the redder or bluer those lines are detected). Then, we relate this “redshift” to time or distances with the help of a cosmological model (the ΛCDM model in this case), or infer distances based on complex calibrations of “standard candles”… no wonder the cosmological model is so extensively tested!
Up until now, all tests the ΛCDM model has faced have been successfully overcome. But it is facing a hard one right now: the so-called Hubble tension. The Hubble constant (H0) is a profound quantity in Cosmology that can be obtained from the six main parameters that describe the current model. To have an idea of its meaning, we can say that it measures the rate of expansion of the Universe and from it, we can obtain the age of the Universe or important insights into the nature of dark matter or dark energy. It was first introduced by Edwin Hubble in the 1920s when he realised that we live in an expanding Universe. The distances to the galaxies he analysed were proportional to its receding velocity, with H0 as the proportionality constant. In other words, he found the relation between redshift and distance that enables the inference of the latter. But, as we have claimed before, getting distances to galaxies is far from trivial. Then, how do we measure H0?
There are two main ways to infer the Hubble constant: through “direct” measurements in the nearby Universe or from the Cosmic Microwave Background (CMD), the faint glow of light that fills the Universe from the epoch of recombination (when photons started to travel freely through space). For the former approach, we need to make use of the “distance ladder”. It is based on the fact that there are objects (“standard candles” such as supernovae, variable stars, etc.) for which we can determine the intrinsic light that they emit, and thus, determine their distance by comparing such intrinsic emission with how faint they are observed. For the latter, we need to assume a cosmological model, once again, the ΛCDM model. And here comes the Hubble tension. Whereas local Universe studies found precise values of H0 of around 74 km/s/Mpc, CMB studies arise even more precise values of ~67 km/s/Mpc, too much of a difference given the small errors associated to those measurements (see figure 2).
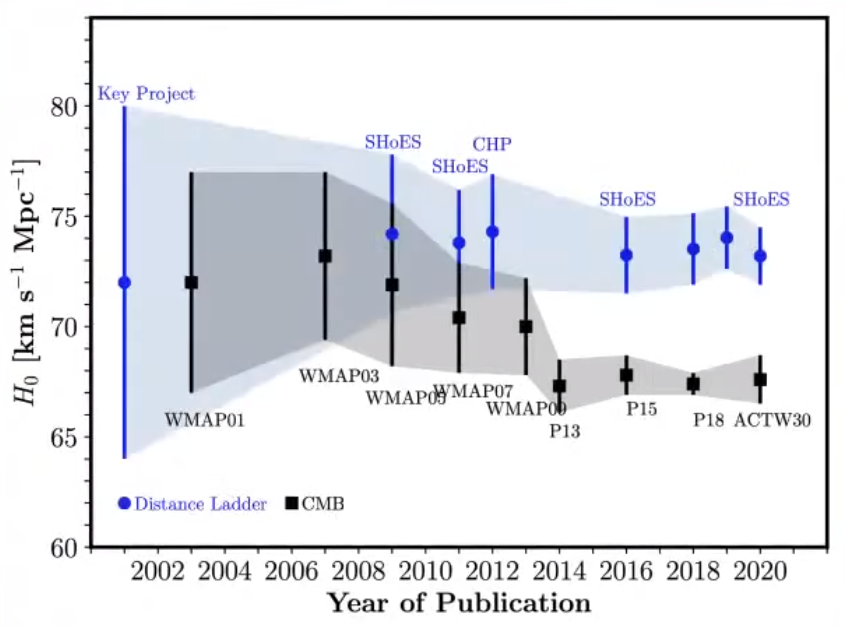
In a recent work led by researchers from the Space Telescope Science Institute and the University of Baltimore 1 , the authors analysed Cepheid variable stars in the galaxies hosting 42 type Ia Supernovae (explosions ignited in binary systems when a white dwarf accretes material from a companion surpassing its critical mass). From their analysis, the authors measured a value for H0 with an unprecedented precision of 73.04 ± 1.04 km/s/Mpc. This means a 5-sigma discrepancy between these results and those from the CMB, or in other words, it seems difficult to reconcile both values. Other studies, making use of other approaches such as the ‘tip’ of the Red Giant Branch 2 (the maximum luminosity of stars with an inert helium core surrounded by a shell of hydrogen fusing into helium) or gravitational waves 3 relax such tension, although always giving values above those measured using the CMB.
But, what does this tension really mean? Remember that we said that observing more distant objects means looking back in time? Well, the CMB was emitted when the Universe was only 400 000 years old, whereas the measurements of Cepheids, SNe, or gravitational waves relate to the local Universe, that in terms of the age of the Universe practically means “now”… does this mean that things were different back then than in the present day? Do we need a new physics or a new cosmological model to reconcile both measurements? Carl Sagan used to say that “extraordinary results require extraordinary evidence” and, as you might have already grasped, this type of analysis is far from trivial. The sources of uncertainty in the data acquisition, analysis, modelling, etc, are overwhelming and, even though we are dealing in all cases with quite precise measurements, we know nothing about their accuracy. True, the measurements have little errors, but are we measuring the correct values? In fact, most of the current work in the field goes in this line, trying to better understand and better analyse the data at hand to walk towards the accurate determinations that we need.
As you can see, we are facing one of the true challenges of, not only the ΛCDM model, but also one of the main pillars of modern Astrophysics, as these differences in the Hubble constant between the current and early Universe attack the very foundations of Astronomy: the cosmological principle. According to this principle the laws of physics are universal and should apply equally to systems nearby (now) and far (past). Stay tuned because it seems exciting science is about to make the headlines of newspapers.
References
- A. Riess; W. Yuan; L. Macri et al. (2022) “A Comprehensive Measurement of the Local Value of the Hubble Constant with 1 km/s/Mpc Uncertainty from the Hubble Space Telescope and the SH0ES Team” , arxiv: arXiv:2112.04510. Link: https://ui.adsabs.harvard.edu/abs/2021arXiv211204510R/abstract ↩
- W. Freedman (2021) “Measurements of the Hubble Constant: Tensions in Perspective”, ApJ, doi: 10.3847/1538-4357/ac0e95. Link: https://ui.adsabs.harvard.edu/abs/2021ApJ…919…16F/abstract ↩
- LIGO and VIRGO collaborations (2021) “A Gravitational-wave Measurement of the Hubble Constant Following the Second Observing Run of Advanced LIGO and Virgo”, ApJ, doi:10.3847/1538-4357/abdcb7. Link: https://ui.adsabs.harvard.edu/abs/2021ApJ…909..218A/abstract ↩
4 comments
Gracias Tomás, este artículo me ayudó bastante para un trabajo de mi Maestría en Astronomía y Astrofísica.
[…] distances to study the pace of the expansion of the universe, especially in the context of the Hubble tension. That’s why it is worth considering taking a look at GRBs, which, as mentioned before, can be […]
[…] se está expandiendo de forma acelerada. Y la culpable de esa aceleración es lo que llamamos energía oscura que, curiosamente, se comporta igual que la constante […]
The Universe expands in an accelerated manner. Therefore, the value of H0 had to be necessarily lower in the past than in the present, as suggested by the author. I recommend to read mi article “Toward a gravitational theory based on mass-induced accelerated space expansion”, published in Physics Essays 35: 258-265 (2022). There I show that the Newton constant G represents the rhythm of accelerated expansion of the space per unit of mass (6.6739×10^-11 m^3 s^-2 kg^-1), which predicts the increase of the H0 value from 400 000 years after the Big Bang to nowadays. This has important implications, as gravitation and accelerated universe expansion seem to derive from the same principle. Therefore, the dramatic accelerated expansion of the space triggered by a high mass density would be the cause of the local bending of the space described by the General Theory of Relativity.