How quantum geometry governs superconductivity in twisted multilayer systems

The band theory of metals has been experimentally tested many times and is now the accepted model of the behaviour of conductors and insulators. Electrical resistance is due to collisions of the electrons (whether treated as particles or waves) with impurities, imperfections, and especially the lattice vibrations of the metal crystal. The lattice vibrations of the solid will decrease as the temperature falls, because the entropy, which represents disorder, also decreases. Therefore the resistance should also decrease. This is what is observed, and it is well explained by quantum band theory.

But at very low temperatures something strange happens: the resistance of some materials suddenly drops to zero at a certain temperature. These materials become superconductors, meaning they can conduct currents without resistance or loss of electric energy. The temperature at which superconductivity occurs is called the critical temperature, T_c. It ranges from 0.015 K for tungsten to as high as 203 K for hydrogen sulfide.

The development of superconducting devices was greatly stimulated after the acceptance of the basic theory of superconductivity proposed in 1957 by John Bardeen, Leon Cooper, and Robert Schrieffer. The authors of the BCS theory, as it is known, received the Nobel Prize for their work in 1972. Their basic idea is that the electron waves in the superconducting state no longer act independently. Instead, they are paired together – the so-called Cooper pairs – at the critical temperature so that their wave functions act as one unit as they interact with the crystal lattice. Moreover, all the electron pairs move together in one collective motion, so that if any single electron is scattered by the lattice it is pulled back into the flow by its partner, and if any pair of electrons is somehow scattered off track, it is pulled back into the collective flow by all the other pairs. Since there is no scattering or inelastic collisions, there is no resistance, and the material becomes a superconductor.

Superconductivity (or superfluidity, the property of a fluid with zero viscosity which therefore flows without any loss of kinetic energy, why this is important in a moment) require bosonic particles to be in the same energy state; in the case of superconductors, these bosons are Cooper pairs – even though electron themselves are fermions (spin ½), when bounded in a pair (integral spin), the pair is a boson.

However, being in the same state is not sufficient. The system needs to be able to host stable supercurrents, that is, dissipationless flow of particles: this is what makes superconductors useful in generating large magnetic fields or in providing qubits for quantum computing. The condensed matter community has long been exploring material candidates to bring superconductivity to room-temperature, high- T_c materials such as cuprates leading the way.

However, a complementary route towards high-temperature superconductivity has begun to emerge, that of purposefully designing materials less complex, and more tunable, than the traditional high- T_c ones, following simple but fundamental theory guidelines relying on flat bands and quantum geometry. Superconductivity has been observed in moiré systems, such as twisted bilayer graphene (TBG), in which the flattening of the electronic band structure occurs at certain twist angles.

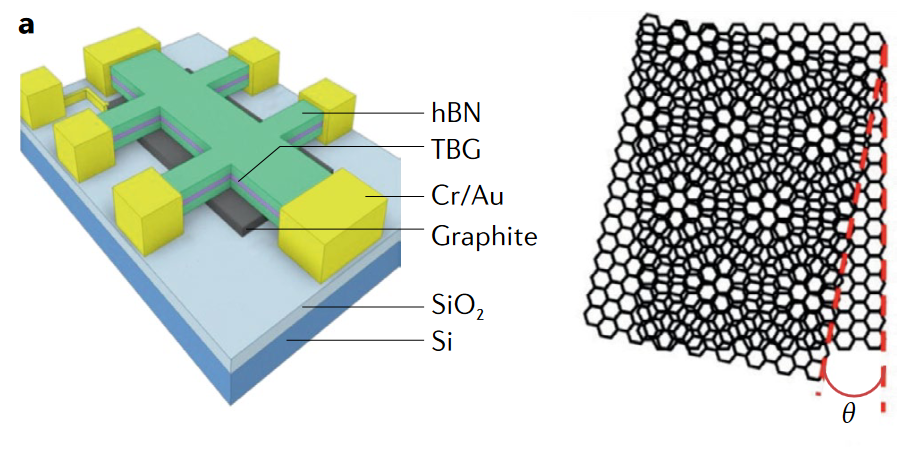
In parallel, theory work has discovered that superconductivity and superfluidity of flat-band systems can be made possible by the quantum geometry and topology of the band structure. These recent key developments are merging into a flourishing research topic: understanding the possible connection and ramifications of quantum geometry on the induced superconductivity and superfluidity in moiré multilayer and other flat-band systems.

A recent review ¹ presents an introduction to how quantum geometry governs superconductivity and superfluidity in platforms including, and beyond, graphene. In this work, the essential theory of quantum geometry dependence of superfluidity is introduced.

The Chern number, an integer, characterizes the topology of filled bands in two-dimensional lattice systems. A band with a non-zero Chern number is topologically non-trivial. The researchers show how a finite Chern number of a band gives a fundamental lower bound of the flat-band superfluid weight, the observable that quantifies the ability of the system to support superfluid transport. Interestingly, a similar lower bound is given by a new type of zero-Chern-number topology in the context of TBG. The team then reviews the theoretical work that predicts the relevance of quantum geometric effects in the experimentally observed TBG superconductivity and other platforms, including ultracold gases.

Finally, the authors sketch the prospects of twisted multilayer systems in providing the route to room-temperature superconductivity. They conclude that a possible sweet spot may exist where quantum geometry effects are maximized by bringing other bands close to the flat band, while keeping them far enough away so that most of the pairing takes place in the flat band, where interactions dominate.

Author: César Tomé López is a science writer and the editor of Mapping Ignorance

Disclaimer: Parts of this article may have been copied verbatim or almost verbatim from the referenced research papers.