Phason dynamics are key to understand electronics in twisted moiré systems

A quasicrystal is a solid structure in which there is long-range incommensurate translational order and a long-range orientational order with a point group. Translated, this simply means that a quasicrystal is ordered but not periodic and, still, it can fill space completely. In two dimensions, the fivefold symmetry of a pentagon is an example of point symmetry, a symmetry that is not allowed by the crystallographic restriction theorem.

Quasicrystals have their own characteristic quasiparticles, called phasons. Phasons exist due to the specific, quasiperiodic lattice structure of quasicrystals. They are somehow similar to a phonon, so let’s recall what a phonon is.

We know that lattice waves may be thought of as elastic waves or simply sound waves, having short wavelengths and very high frequencies, which propagate through a crystal at the velocity of sound. The vibrational thermal energy for a material consists of a series of these elastic waves, which have a range of distributions and frequencies. At the atomic scale, quantum phenomena become apparent. Hence, only certain energy values are allowed. Einstein’s famous predictions for the behavior of the specific heat of solids as a function of temperature, for instance, were based on an application of the quantum hypothesis to a model of a crystalline solid in which the lattice atoms behave as three-dimensional oscillators vibrating with quantized energies. So, a single quantum of vibrational energy is called a phonon. On occasion, the vibrational waves themselves are termed phonons.

Whereas phonons are related to translation of atoms (vibrations), phasons are associated with atomic rearrangements. As a result of these rearrangements, waves, describing the position of atoms in a crystal, change phase, thus the term phason.

Consider now twisted moiré systems like twisted bilayer graphene, what effect would be a better descriptor, phonons (vibrations) inherited from each layer or phasons arising from the rearrangement of atoms due to the relative position of the layers?

The elastic collective modes of a moiré superlattice arise not from vibrations of a rigid crystal, but from the relative displacement between the constituent layers. The moiré pattern is a sixfold symmetric incommensurate superlattice and not a rigid crystal. As a result, its low-energy elastic excitations are not described by acoustic phonons, but by phasons.

The crucial difference is that, while the dispersion of acoustic phonons is governed by the conservation of linear momentum of the ions of a rigid lattice, phasons in twisted bilayer graphene are related to the relative translation between the layers, which is not a symmetry of the system since the layers are subjected to adhesion forces.

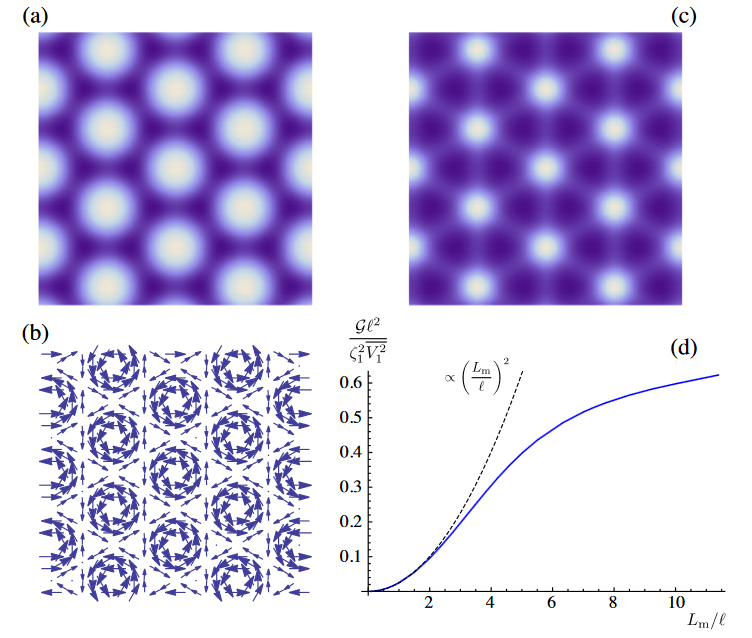
Now, Héctor Ochoa and Rafael M. Fernandes show ¹ that random forces affecting the relative orientation and displacement between the layers, no matter how small they are, give rise to a characteristic length scale beyond which stacking order is lost. Thus, this length scale, which depends on the elastic constants of graphene and on the strength of the disorder potentials, is the one associated with twist-angle inhomogeneity.

In other words, disorder in the relative orientation between the layers and thermal fluctuations associated with their sliding motion degrade the propagation of vibrations in the moiré superlattice; the phason modes displaying a universal dependence on the twist-angle variance.

Experimentally, the phason dynamics should be manifested in thermodynamic properties at low temperatures, such as in the specific heat capacity. Importantly, inhomogeneous twist angles have been widely observed in twisted bilayer graphene devices and shown to strongly influence the electronic properties. This could be interpreted as a result from the electron-phonon coupling in which the changes in the phason modes promoted by twist-angle variations will inevitably impact them in different ways.

Author: César Tomé López is a science writer and the editor of Mapping Ignorance

Disclaimer: Parts of this article may have been copied verbatim or almost verbatim from the referenced research paper/s.