Simple explanations for some complex patterns in twisted bilayer graphene

Twisted bilayer and multilayer systems represent two-dimensional materials, where atom-thick layers of the same or different materials are superimposed and rotated by an arbitrary twist angle. Twisted bilayer graphene (TBG) represents arguably the most prominent physical system of this kind, the bilayers of transition metal dichalcogenides (TMD) the other. The effect of twisting two periodic systems with respect to each other results in the formation of superlattices, the moiré patterns. In TBG, a moiré pattern forms that introduces a new length scale to the material. At the “magic” twist angle of 1.1^∘, this causes a flat band to form, yielding emergent properties such as correlated insulator behaviour and superconductivity.

Strains are ubiquitous in moiré systems. While the effect of strains in monolayer graphene and other non-twisted bidimensional materials has been extensively studied, the interplay of electronic and elastic degrees of freedom in moiré systems is not fully understood. Some important insights on the role of strains in twisted bilayer graphene have been reported, though. The applied in-plane strain acting on both sublattices in opposite directions changes the distance between the nearest lattice atoms within each layer, and increases correspondingly the electronic hopping amplitude between them.

In terms of the effective Dirac description of graphene, this effect creates an additional term which resembles the conventional vector potential, which however does not break the time-reversal symmetry of the Hamiltonian. This term displaces the Dirac points from their original positions but does not distort the shape of the Brillouin zone. This process breaks the C6-symmetry of the Dirac points and lifts the degeneracy of the saddle points.

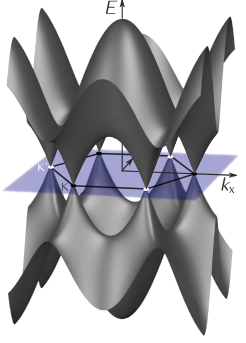
At larger strains the system goes through a Lifshitz transition characterized by a fusion of the Dirac points with the resulting anisotropic spectrum and different scaling behaviour of the low-energy part of the density of states.

Similar effects might be expected for strained twisted bilayer graphene, such as the appearance of higher van-Hove singularities. However the plethora of observed phenomena in strained twisted bilayer graphene is much larger than suggested by those analogies. For instance, the observation of highly anisotropic moiré patterns in the strained twisted bilayer graphene has been reported in many experiments. With increasing strain, the degree of deformation of the unit cells increases as well, until they become effectively one-dimensional stripes.

Now, a team of scientists shows ¹ how the deformation of the moiré superlattice, and the emergence of quasi-one-dimensional features is a consequence of the interplay between twist and strain.

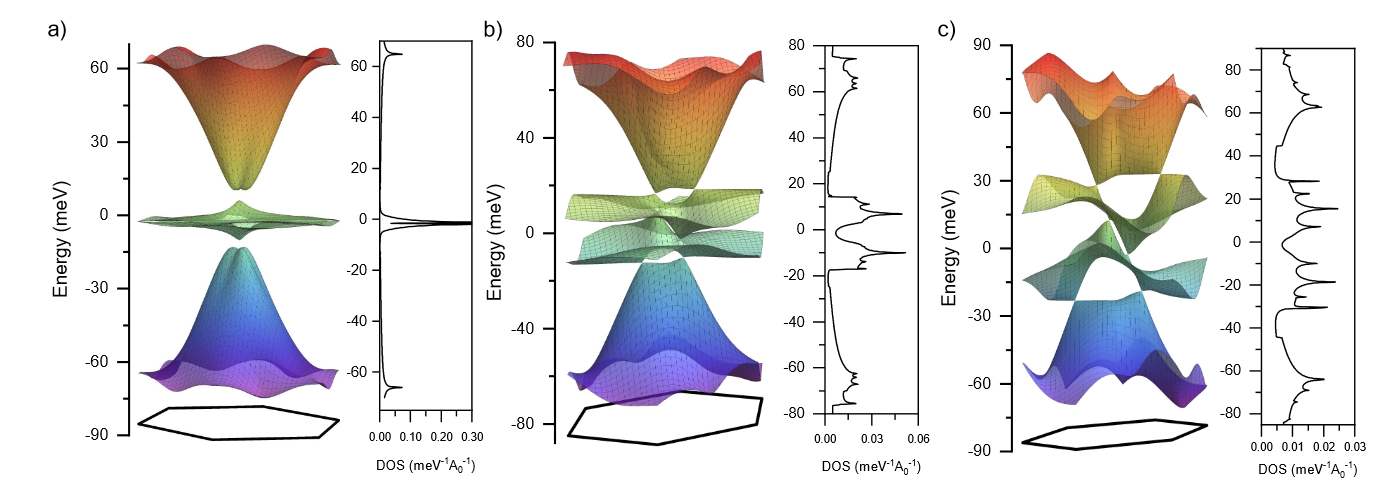
As a criterion for such transition, the researchers find a simple relation between the applied uniaxial strain, the twist angle, and the material dependent Poisson ratio. Initially, the Brillouin zone has the form of a perfect honeycomb cell. With increasing strain, it gets deformed and elongated in a selected direction, until it reduces to a line at the critical strain value. The selected direction is determined by the material dependent parameters.

The team builds the strain dependent lattice vectors in both real and reciprocal spaces and explore the consequences of this transition for the spectra and the density of states of twisted bilayer graphene within a continuum model approximation. In the one-dimensional limit, they obtain electronic bands, which are determined by an interplay of two generally different and incommensurate periodicities. These can be fine-tuned to a single periodicity by varying external applied forces.

These results offer simple explanations for the complex patterns of one-dimensional channels observed in low angle twisted bilayer graphene systems and twisted bilayer dichalcogenides. They can be applied to any hexagonal twisted moiré pattern and easily extended to other geometries.

Author: César Tomé López is a science writer and the editor of Mapping Ignorance

Disclaimer: Parts of this article may have been copied verbatim or almost verbatim from the referenced research paper/s.