27% of all materials in nature are topological. And now there is a catalogue

Topological materials have special universal properties, which are protected against perturbations. Such properties are theoretically described by topology, a branch of mathematics concerned with the properties of geometrical objects that are unchanged by continuous deformations. Topological materials behave like an ordinary insulator in the bulk but have conducting states on their boundaries, i.e., edges or surfaces. The conducting surface is not what makes topological materials unique, but the fact that this surface state is particularly robust.

In 2017, a giant step was taken towards the understanding of topological materials with the publication of a paper in Nature called Topological Quantum Chemistry (TQC), ¹ as it meant the completion of the theory of electronic band structure. As the editor put it: “[…] a new and complete theory for calculating the topological properties of the electronic band structures of materials. […] The theory should greatly simplify the search for further materials with exotic properties and also shed light on the underlying physics of existing topological materials.”

Now, as a continuation of this work, almost the same team members, in this case with Ikerbasque Researcher Maia Garcia-Vergniory (UPV/EHU, DIPC) as first author, present ² a new database to identify the topological classification of any material. This database allows users to select elements from the periodic table to form a compound that can then be explored for its topological properties.

How many topological materials exist in nature? What are they? What is their abundance? The remarkable field of topological insulators and semimetals has combined deep theoretical insights with almost immediate material predictions and their experimental discovery. Since the start of the field 13 years ago, the prevalent impression in the physics and chemistry community is that topological materials represent an infinitesimal proportion of the whole number of materials existing in nature. Even though it led to a comparatively large number of successes, the method of predicting new topological classes and corresponding materials is at the moment mostly based on educated guesses.

In TQC, the researchers first compiled all the possible ways energy bands in a solid can be connected throughout the Brillouin zone to obtain all realizable band structures in all non-magnetic space-groups. Group theory itself places constraints – “compatibility relations” – on how this can be done. Each solution to these compatibility relations gives groups of bands with different connectivities, corresponding to different physically-realizable phases of matter (trivial or topological).

The scientists solved all compatibility relations for all 230 space groups by mapping connectivity in band theory to the graph-theoretic problem of constructing multipartite graphs. Then they developed the tools to compute how the real-space orbitals in a material determine the symmetry character of the electronic bands. These elementary band representations allow to easily identify candidate semimetallic materials. (Figure 1)

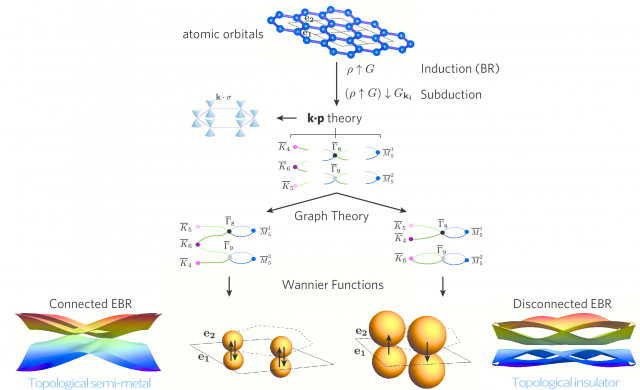
What they have done now is using TQC to present a large list of the (strong) topological (nonmagnetic) “high-quality” materials in nature, along with a wide array of information about their structure, bands, and topological properties.

This extensive work is composed of several research modules, presented in Figure 2, each of which is essential for finding the materials with strong and fragile topology in the Inorganic Crystal Structure Database. The researchers developed several codes to compute all characters of all symmetries of materials and to identify new topological phases.

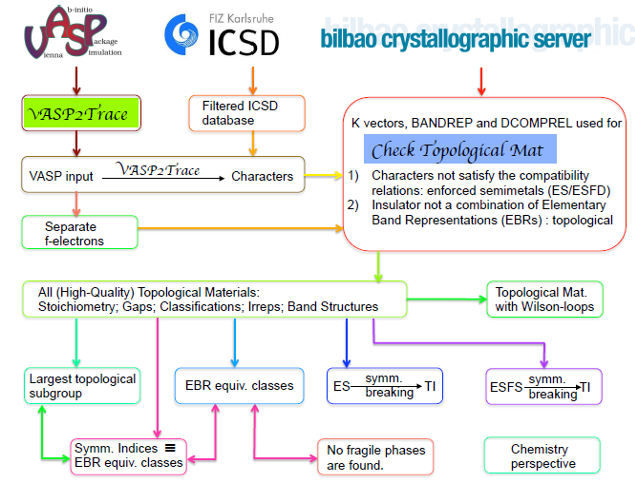
Out of 26938 stoichiometric materials, 3307 topological insulators and 4078 topological semimetals and 0 fragile phases were found . For these 7385 materials the electronic bands structure – including some electronic properties (gap, number of electrons), the symmetry indicators, as well as other topological information – are provided.

But probably the most surprising result is the aggregate: more than ¡27%! of all materials in nature are topological.

The team’s open-source code on the Bilbao Crystallographic Server, “VASP2Trace”, and end-user button “CheckTopologicalMat” are both available online. You can check the topology of any material or reproduce these impressive results.

Author: César Tomé López is a science writer and the editor of Mapping Ignorance.