Quantum worlds from scratch: Synthetic matter in nonstandard geometries

Quantum simulation, a concept that once seemed like science fiction, is now revolutionizing the way physicists study the quantum world. The idea, famously suggested by Richard Feynman in the 1980s, is to use a controllable quantum system to mimic the behaviour of another system that is too complex to study directly. Over time, researchers have developed various platforms—ranging from ultracold atoms to photonic lattices and engineered electronic materials—that make this idea a reality. Initially, these simulators aimed to replicate known materials and physical models. But the field has now taken a bold turn: exploring quantum systems that do not, and perhaps cannot, exist naturally.

Synthetic matter, inventing new quantum realities

A recent in-depth review ¹ brings this emerging direction into focus. The paper is not merely a catalogue of recent experiments—it’s a roadmap to a new frontier in quantum simulation: synthetic quantum matter in nonstandard geometries. These are systems that exist beyond the constraints of conventional three-dimensional Euclidean space, incorporating fractal structures, quasiperiodic lattices, higher spatial dimensions, and even curved space that mimics general relativity. This is a leap from simulating nature to inventing entirely new quantum realities.

To appreciate what makes these systems so exciting, it helps to begin with what is meant by “nonstandard geometry.” Most materials, and most physics as we know it, exist in spaces that are flat and periodic. Atoms in a crystal, for example, are arranged in repeating patterns in three-dimensional space. But what happens if the underlying space is not flat or not periodic? What if it has curvature like the surface of a sphere or a saddle, or structure like a fractal that repeats on smaller and smaller scales without ever becoming truly regular? These questions are no longer just mathematical curiosities—they are now testable through experimental setups in the lab.

Quasicrystals

Quasicrystals are one of the most studied examples of nonstandard geometry. These structures are ordered but not periodic. First discovered in the 1980s in certain metallic alloys, quasicrystals exhibit symmetries that were previously thought impossible in solid matter, such as fivefold or tenfold rotational symmetry. What distinguishes them from random or disordered systems is that they follow deterministic rules, often based on mathematical sequences like the Fibonacci series, which give rise to long-range order without repeating. In quantum simulations, these quasicrystalline arrangements enable researchers to probe the delicate interplay between order, disorder, and localization. They also allow for the emergence of exotic topological phases of matter that are not accessible in conventional periodic lattices.

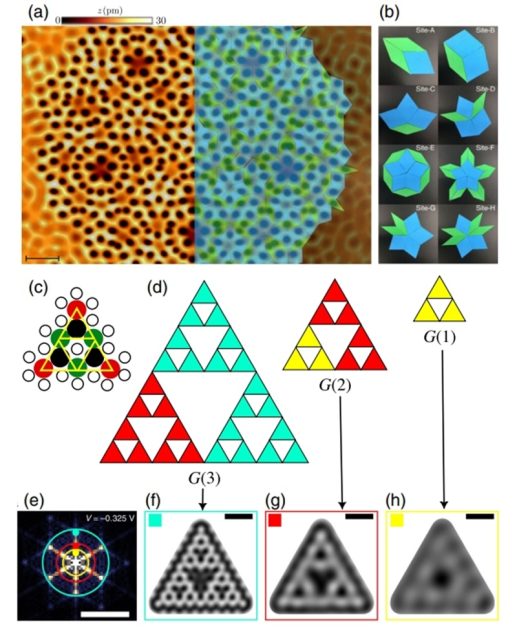
Fractals

Fractals, another category of nonstandard geometry, bring an entirely different set of properties into play. Defined by self-similarity and non-integer dimensions (known as Hausdorff dimensions), fractals like the Sierpiński triangle or Sierpiński carpet are more than just beautiful mathematical constructions. When quantum particles are confined to move on such fractal lattices, their behaviour deviates from the norms established in one, two, or three dimensions. Quantum states in these systems may exhibit critical localization, where the wavefunction is neither completely localized nor fully extended. This is a regime that challenges many existing theories and opens new possibilities for understanding quantum transport.

Higher spatial dimensions

Even more abstract are systems that simulate higher spatial dimensions. While humans experience three dimensions of space, mathematical physics has long explored theories in four or more dimensions. In quantum simulations, these extra dimensions are constructed synthetically. For example, internal atomic states can be coupled together in a way that mimics spatial connectivity, effectively creating a “synthetic dimension.” When combined with real spatial dimensions, this allows experimentalists to simulate four-dimensional spaces. One of the most striking results from such simulations is the observation of the 4D quantum Hall effect, a phenomenon with no counterpart in the physical three-dimensional world, characterized by topological invariants like the second Chern number.

Curved space

Curved space, a familiar concept from general relativity, also finds a home in quantum simulators. Although we cannot bend the vacuum of space in a lab, researchers can simulate the effects of curvature by engineering spatially varying interactions or hopping amplitudes in optical lattices. Some experiments mimic an expanding universe using a Bose-Einstein condensate in a time-dependent trap, observing redshift-like effects analogous to the stretching of space in cosmology. Others explore analogues of black holes and cosmic strings using strained photonic lattices or inhomogeneous condensates. These setups provide rare experimental insight into the behaviour of quantum fields in curved spacetime, a subject that is otherwise extremely difficult to probe.

Variety of platforms

The variety of platforms used to realize these geometries is equally impressive. Ultracold atomic systems offer a high degree of control over interactions and lattice configurations. Lasers can be used to form optical potentials that trap atoms in precise, programmable arrangements. Optical tweezers take this a step further by positioning individual atoms one by one, enabling the construction of arbitrary patterns, including fractals. Photonic systems, where photons are confined in waveguides or microcavities, provide another rich arena. In these systems, modulating the physical or refractive geometry allows for the emulation of complex lattices and topologies. Even electric circuits have entered the game: networks of capacitors and inductors can simulate tight-binding models, including those with topological or hyperbolic features. Circuit quantum electrodynamics systems, using superconducting qubits and resonators, can emulate interacting quantum systems in geometries that go far beyond what naturally exists.

The role of geometry and topology

The payoff from all of this engineering is not just technical—it’s conceptual. Many of the most intriguing phenomena in modern physics are deeply tied to geometry and topology. For instance, the way electrons move in a material, whether they scatter, localize, or flow without resistance, depends not just on the strength of interactions but on the underlying geometry of the space they inhabit. In synthetic quasicrystals and fractals, localization can occur even in the absence of disorder, challenging traditional views of quantum transport. In higher-dimensional lattices, new classes of topological insulators emerge, supporting edge modes and quantized responses that defy conventional classification. And in curved quantum simulators, one can mimic gravitational horizons, potentially offering insights into fundamental problems like Hawking radiation and the Unruh effect.

Unexplored territory

What makes this entire field especially exciting is its forward-looking nature. The systems being studied do not simply reproduce known materials or models—they venture into unexplored territory. In doing so, they create a new form of quantum matter, one not constrained by the natural world but instead crafted by human ingenuity. These synthetic systems act as a kind of telescope turned inward, offering a glimpse into alternate quantum realities and deepening our understanding of what quantum matter can be.

The study of synthetic quantum matter in nonstandard geometries marks a profound shift in the goals of quantum simulation. Rather than merely mimicking nature, researchers are now building quantum worlds from scratch—worlds with strange dimensions, fractal rules, and curved spaces. In these worlds, the boundaries between condensed matter, high-energy physics, and cosmology begin to blur, offering a new platform to address some of the most fundamental questions in science. This is not just a step forward for quantum physics—it is a leap into the quantum unknown.

Author: César Tomé López is a science writer and the editor of Mapping Ignorance

Disclaimer: Parts of this article may have been copied verbatim or almost verbatim from the referenced research paper/s.