Quantum Thermodynamics VI: Negative absolute temperatures in optical lattices

As we have discussed in our previous post, there is an important debate in the scientific community regarding the existence of negative absolute temperatures. The debate is not over, and both sides have valuable arguments, but in any case, one thing has already been proved. If negative absolute temperatures are real, the requirement to achieve them is to have a system where the energy is bounded from above. In our normal, macroscopic world, this is not the case. For instance, kinetic energy has a minimum value when particles are at rest, but it has no maximum. To find systems with an upper energy bound we need to explore the microscopic world.

The first kind of systems used to generate negative absolute temperatures was localized spin systems. This was a natural choice. Spin is an intrinsic magnetic moment of atoms that can have only certain discrete values. If there is an external magnetic field acting on the system the energy different spin configurations present different potential energies. If all spins are aligned with the external field, the energy is minimum, and if all the spins in the opposite direction we find the maximum energy. This means that the system has minimum and maximum energies. This kind of systems was already studied during the fifties proving that the spin distributions are equal to the predicted by Boltzmann’s distribution with negative absolute temperatures ¹.

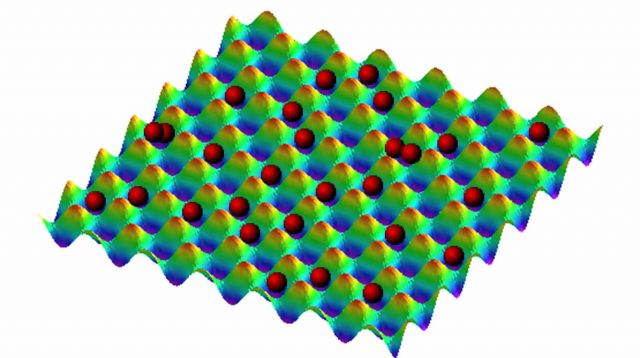
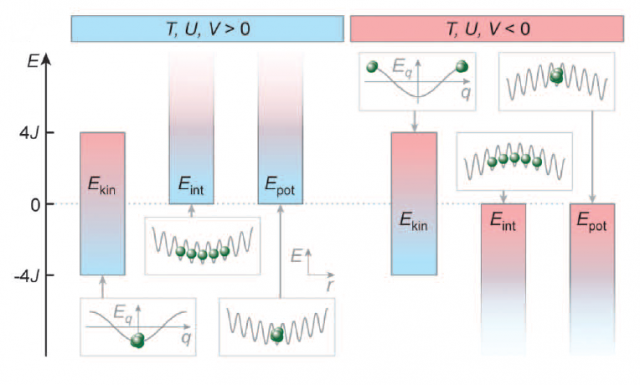
More recently, a new experiment has showed negatives temperatures in a more complicated and interesting system ². The system under study was composed by confined atoms in an optical lattice. Optical lattices are a popular way to confine and control atoms. They are prepared by laser interference that leads to an interference energy pattern. The atoms are located at the minimum potential sites of this pattern (see Figure 1). This is a quantum system, and the kinetic energy of the atoms is discretized. If the potential barriers are sufficiently deep it is fair to assume that the atoms cannot reach a high-energy state. Under this assumption, the kinetic energy has a minimum and a maximum, and the dynamics of the system is described by the Bose-Hubbard model. This model has three parameters (J, U, V). J is the parameter associated with the capacity of the atoms of jumping between neighboring sites, U is the parameter that determines the energy of each site as a function of the number of atoms that occupy the site, and V represents an external harmonic potential that makes some sites more energetic than other. There are also three types of energy, a kinetic energy, that is upper and lower bounded, an interaction energy due to the atom-atom interaction, and a potential energy due to the external potential. If the potential and interaction energies are upper or lower bounded depends on the parameters U and V. In Figure 2 the energy diagrams of the system are shown for both positive and negatives values of the parameters. It is clear from the picture that if U and V are negative all the energies have a maximum and the temperature of the system (by using Boltzmann’s definition) is negative.

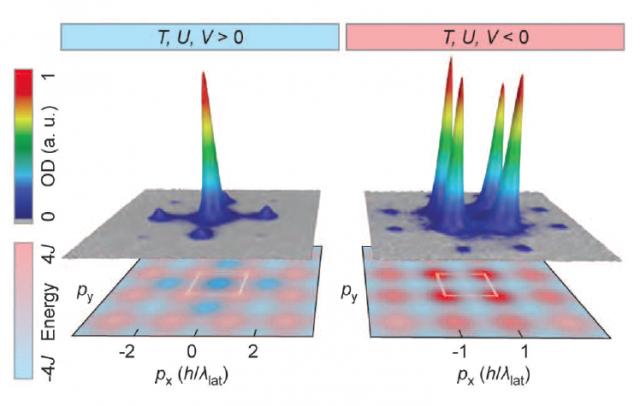
Luckily, the parameters of the Hubbard-Bose Hamiltonian can be controlled, and the transition between positive and negative temperatures is possible. The experiment was performed with a Bose-Einstein condensate of 10⁵ potassium atoms. Negatives temperatures were not directly measured, but the experimenters measured the velocity distribution of the atoms proving that the system was in a repulsive state. The momentum distributions for attractive and negative systems are displayed in Figure 3. These distributions are also the same that are predicted by Boltzmann theory with negative absolute temperatures

Another interesting feature of this system at a negative temperature is that it should have negative pressure too. This is of interest to the study of cosmology, as negative pressures are necessary to explain the accelerating expansion of the universe. Because of that, this system can also be used to simulate and study cosmological problems.

The experiment did not directly proved the existence of negative absolute temperatures. It proved only that this system could reach such a temperature under the assumption that Boltzmann’s entropy is correct. The critics of negative temperatures consider that if Gibbs’ entropy is the correct one, even a system with upper bound energies has a positive absolute temperature. As we said in the previous post the debate is not over, and this kind of experiment cannot help us to determine which side is right, at least until now. In the future, a more direct analysis of the temperature of these systems is desirable. This goal can be achieved by different means. For example, as a negative temperature is hotter than all positive temperatures, if this system is in contact to any positive temperature system the temperature of this should increase. Even more interesting would be to use this system to create a heat machine with efficiency higher than one. All these potential applications have important difficulties. First, the system requires a high isolation from the environment to create the Bose-Einstein condensate. This means that if the system is in contact with any another system its properties can change, changing, therefore, its temperature. Second, the stability lifetime of the system is very short; it is of the order of microseconds. This represents enough time to perform these measurements, but engineering any kind of thermal machine is not plausible. Third, the energy contained in the system is very small, as there are only hundred thousand atoms in it. Because of that, even if it were in contact with another system the temperature of this system would increase very slightly.

A direct measure of the temperature of the system or of its thermodynamic properties is still to come. This is the best way to put some light in the debate about the reality of negative absolute temperatures.