Quantum Thermodynamics IV: Negative absolute temperatures

Almost everyone with basic knowledge of physics have one clear concept, there is a minimum temperature and it is called ‘absolute zero’. This temperature corresponds to -273.15 degrees in the Celsius scale. In the Kelvin or absolute scale it is zero, by definition. Furthermore, there is another idea that is also widespread: absolute zero is unreachable.

Recently, the minimum temperature record in the known universe has been beaten. This milestone has been performed by CUORE collaboration, an international group formed by 130 scientists. They have reached -273.144 C, only 0.006 degrees above absolute zero. On the other hand, as absolute zero is unreachable, we can also consider that we are still infinitely far away from it. The closer we get the more difficult becomes to keep reducing the temperature.

Hence, if absolute zero is unreachable it is natural to think that there are no negative temperatures in the absolute scale. But this point is not so clear, and it is an interesting matter of debate nowadays. Using an analogy, something similar happens with the speed of light. It is known, by Einstein’s special relativity, that you can not accelerate a body to the speed of light by applying a force to it. What relativity does not explicitly forbid is to create a particle with a speed faster than light, what is called a tachyon. Why then do most of the scientist say there are not such supraluminical particles? This skepticism comes from the fact that if tachyons do exist, they could be used to perform many counterintuitive tasks, like time traveling. Something similar happens with negative temperatures. Absolute zero is unreachable, but thermodynamics does not explicitly forbid to create a system with a negative temperature. It is even more tricky than the example of the speed of light, because negative temperatures are not really below absolute zero. They are indeed hotter than any positive temperature, meaning that they are above infinite temperature (see Figure 1). As faster than light particles, negative absolute temperature systems also allow many processes that positive ones do not, like achieving an efficiency greater than one in a heat machine.

As said before, the existence of negative absolute temperatures is still a matter of debate. To discuss about this we need to define first what ‘temperature’ means. It is definitively a complicated concept. We all have an intuitive definition of temperature but its mathematical definition is not so simple. To define it we need to first discuss another thermodynamical concept, entropy.

Entropy is the key magnitude of statistical physics, the key concept that relates the microworld, of atoms and molecules, with the macroworld where we live. It was first defined by the Austrian physicist Ludwig Boltzmann. To understand entropy we need to define the concepts of micro and macrostate. The macrostate of a system is what we can observe in our macroscopical world. Examples of macroscopic quantities are temperature and pressure. From a thermodynamics point of view, a macrostate is defined by these quantities. On the other hand, the microstate can only be defined by stating all the parameters regarding the atoms and molecules in the system. Let see a canonical example. In a classical atomic gas, with no quantum effects, the macrostate is determined by pressure, volume, temperature and mass. Defining the microstate requires to specify the positions and velocities of all the atoms (usually the number of atoms is of the order of Avogadro’s number 6.022 x 10^23).

Many different microstates can lead to the same macrostate. Following the previous example, there are many ways of placing the atoms of a gas that lead to the same values of the volume. Entropy is just a way of counting the number of microstates that correspond to the same macrostate. The entropy of a certain macrostate is proportional to the number of its compatible microstates. Hence, if we fix the energy of a system, it will evolve to the macrostate with maximum entropy, meaning to the macrostate with the larger number of microstates compatible with it.

We can jump now to the mathematical definition of temperature. Temperature is defined as the variation of entropy in a system when its energy changes. In most of the systems there is a minimum energy, but there is no maximum. Think again in our atomic gas example, in this case there is a minimum energy, meaning all the atoms at zero speed (be aware that we are not considering quantum effects). For this kind of bounded states entropy always growths with the energy, leading to a positive temperature in any case. But what happens in a system with a maximum of energy? In this other case, there is the possibility of having an entropy that decreases with the energy, leading to a negative temperature. In Figure 3 we can see a diagram of the entropy behavior as a function of energy in all possible regimes.

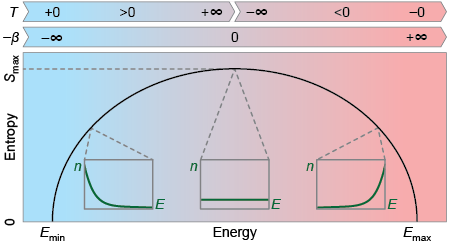
Let state some interesting features about negative temperatures. Positive and negative are totally arbitrary concepts regarding temperatures, meaning that negative temperatures are not below absolute zero. They are indeed temperatures above infinite, meaning that a body with a negative temperature should always give energy if it is in contact with another one at positive temperature. Everything looks simpler if instead of temperature we use its inverse to define the state of a system. In this case there is no discontinuity, and the transition from positive to negative temperatures is smooth as it is displayed in Figure 3. Absolute negative temperatures also challenge classical Thermodynamics, as they allow the construction of heat engines with efficiencies higher than one and perpetual mobile machines.

The idea of negative temperatures is not new. First measures of them were reported already by Purcell and Pound in 1951 in nuclear spin systems ¹, and their thermodynamic implications were discussed by Ramsay in 1956 ². Recently, Dünkel and Hilbert have considered³ that the existence of negative absolute temperatures is unphysical and inconsistent with Thermodynamics. They claim that negative absolute temperatures are just a mathematical consequence of using Boltzmann definition of entropy, that is inconsistent. They present some examples were the use of Boltzmann entropy leads to unphysical results and they propose an alternative, Gibbs entropy.

Gibbs entropy ⁴ is only slightly different than Bolztmann’s. As we have already said if we have a fixed energy, Bolztmann entropy is proportional to the number of microstates within this energy. Besides, Gibbs entropy depends not only in the microstates with this energy, but also in all the microstates with an energy smaller than this one. This difference is very small for very big systems, because in this case the number of states increases with the energy in such a way that the number os states with a certain energy is almost equal than the number of states with an energy smaller or equal that this energy. This could be consider counterintuitive but when we deal with very big numbers, as the number of atoms in a gas, intuition is not a good guide. Gibbs entropy always increases with energy, meaning that the temperature is always positive, even in the case of upper bounded systems.

This is not the end of the story because there are also two recent critics to Ref [4]. First, there is a paper⁵, accepted for publication in the American Journal of Physics, criticizing Dunkel and Hilbert conclusions. The main argument of this paper is that in Dunkel and Hilbert example of a system were Boltzmann entropy leads to unphysical results is far from thermodynamics regime, as these results are obtained only for small number of particles. They conclude that when the number of particles increases Boltzmann entropy gives always physical results. They also proposed an example of two systems that are at thermal equilibrium but they present different Gibbs temperatures, contradicting Thermodynamics. The authors of the original paper [4] have replied by writing a comment to Ref. [6] that is still unpublished ⁶. They argue that the conclusions about Gibbs temperature are based in approximate calculations, and that this cannot contradict exact results.

The other main publication criticizing Gibbs entropy is a comment ⁷ to Dunkel and Hilbert’s Ref.[4]. At the moment of writing this post this comment is still unpublished. The authors of the comment claim that Gibbs entropy leads to many unphysical results. One of them is that it cannot be calculated just by the state of the system, because you need to take into account states and energies that the system does not reach. Some of these states do not even represent a physical state. Also, they say that this entropy is ill defined in the thermodynamical limit (when the number of particles is infinite) and that it violates the Second Law of Thermodynamics. Finally, there is also a reply to this comment ⁸ referring to old papers and books to disprove all these critics.

Due to the active discussion we can only conclude that the existence of negative absolute temperatures is still under debate. Definitively, if they do exist they represent a huge opportunity for science and technology. At the end, as physics is an experimental science, the discussion should be closed by experiments. If negative absolute temperatures are real some of the cool things they can do should be doable. At the moment, there are some different experiments that have claimed to measure such temperatures, all by using Boltzmann definition of entropy, but none of them has really challenged classical Thermodynamics. Most of these experiments use quantum systems to create upper bounded systems, and this will be the topic of our next post.