Quantum kisses between optical nanoantennas

The wave nature of light expresses itself in the propagation all over space, showing an intrinsic limitation to be localized beyond the so-called diffraction limit which is of the order of half the wavelength of the photons propagating. However when interacting with matter, light often gets reflected, diffracted, scattered or absorbed depending on the interactions and excitations induced in the material. In particular, at visible wavelengths, between 450 nm and 800 nm, metals interact with electromagnetic waves producing a variety of optical effects. The conduction electrons that constitute the metal can oscillate rigidly at certain optical frequencies that depend on the electron density. Furthermore, when metals are physically bounded by surfaces and interfaces as it is usually the case in nanoparticles and nanostructures, the oscillations of the electron charge density at the surfaces show resonant localized modes so-called surface plasmons. The excitation of these surface plamons by light produces a localization and enhancement of the visible light at the surface of the metal at distances of a few nanometers, well below the diffraction limit, thus acting metallic nanostructures as resonant emitters or receptors of light. This is the reason why metallic nanostructures are often referred to as optical nanoantennas.

An example of the simplest optical nanoantenna one can think of is shown in Fig. 1a. A metallic nanoparticle enhances both the absorption and the scattering of visible light acting as an isotropic optical nanoantenna. The spectrum of scattering and emission (Fig.1b) shows a distinctive resonance or antenna mode sustained by the excitation of localized surface plasmons.

In the last years, the development of sophisticated fabrication techniques that range from electron beam lithography to wet chemistry synthesis, together with the improvement of optical characterization techniques allowing for accessing far-field as well as near-field properties in the nanoscale have made possible to study ultrafast processes and nonlinear phenomena induced by intense light pulses. In parallel, new theoretical frameworks have been developed to describe the main features of the complex physical processes involved in the interaction between light and matter, boosting tremendously the field of plasmonics ¹.

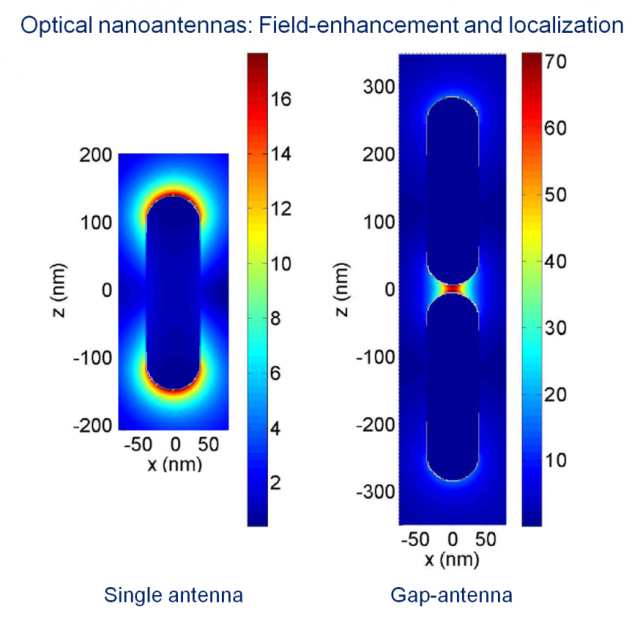
Simple optical antennas have been developed in the last years relying on canonical structures such as spherical nanoparticles, nanorods, nanorings, nanoshells, metallic dimers, etc. The optical antenna resonances produced at the particles depend not only on the shape and particular material of the nanostructure but it is also strongly affected by the Coulomb interaction between different nanostructures. A gap nanoantenna is typically composed of two metallic arms or electrodes that interact through a vacuum gap between them where strong electrical coupling is produced modifying the response of the whole system and producing a red-shift of the optical response as the antenna arms approach closer together ². In this situation, the properties of a very small portion of space at the gap, typically a few nanometers, govern the behavior of a huge amount of electrons spread over the particles setting the energy of the resonances and their corresponding electric field distributions. An example of such situation is shown in Fig. 2 where the near-field response of rod-like metallic nanoantennas is shown both for a single and a gap antenna. The electromagnetic coupling between two antennas forming a gap produces an extreme subwavelength localization of the field and a dramatic enhancement of its amplitude. The main features of this effect can be described within the framework of classical Electrodynamics where hybrid resonances are determined by this Coulombic coupling of the oscillating surface plasmons (classical harmonic oscillators).

However as the separation distance between nanoparticles in a gap-nanoantenna is reduced to subnanometric distances, the quantum nature of the electrons in the particles takes a predominant role in determining the optical response of the system. It is necessary to go beyond a classical description of light-matter interaction -usually addressed through the macroscopic polarization of objects- in the framework of classical Maxwell’s equations. The microscopic nature of the conduction electrons, their complex many-body interactions and their response to incoming light is best addressed in the framework of quantum mechanics, where all the non-local interactions between the thousands of electrons collectively oscillating can be properly accounted for ³. One of the schemes to resolve the quantum mechanical response of the electrons relies on the description of the energetic of the electrons through their electron density and the further trace of how this density responds in time to a perturbation such as a light pulse. This is commonly addressed within time-dependent density functional theory (TDDFT). When the quantum nature of the electrons is considered, the non-local interactions between the electrons within each nanoparticle are naturally included in the response, and furthermore, if located close enough, electrons from one nanoparticle can tunnel into the other particle by means of a quantum coherent process of tunneling. This effect is schematically depicted in Fig. 3: driven by the exciting light pulse, a few electrons can tunnel forth and back during each optical cycle modifying the optical response of the whole system.

As a consequence of quantum effects thus, the optical spectrum of a gap-nanoantenna can be dramatically modified when two particles are located at subnanometric proximity. According to the last calculations of the teams at the Center for Materials Physics (CSIC-UPV/EHU) and DIPC in Donostia-San Sebastian, Basque Country, together with Andrei Borissov at the Université Paris Sud in Orsay, France, and Peter Nordlander in Houston, USA, for separation distance below 4Å between the particles, tunneling is triggered out changing the distribution of the surface charge densities, i.e. modifying the plasmonic antenna resonances, and thus quenching the maximum electric field enhancement at the gap [3]. This effect has important implications in the design of optoelectronic devices as well as in nanoantenna-enhanced spectroscopy targeting sensing at the single-molecule level, since the intense field enhancements allowing high performance of field-enhanced spectroscopies can be compromised due to quantum effects (tunneling killing the field enhancement).

To address quantum effects in large plasmonic antennas is very challenging due to the huge amount of electrons at each nanoparticle involved in the oscillating response to light. The teams in San Sebastian, Paris and Houston have developed a hybrid model to describe quantum effects in a cavity together with the classical response of the rest of electrons in the nanoparticles forming a nanoantenna. This quantum-corrected model (QCM) has allowed for describing quantum tunneling and spill-out of electrons while giving account of the spectral features of the whole antenna. In Fig. 4 we apply the quantum-corrected model to describe the quantum “touch” between two large nanoparticles of 50 nm in size. The distribution of modes of the two interacting particles is shown as a function of separation distance between them. The response of the far-field (extinction of light) of the two-particle system is shown as calculated in a classical framework (Fig. 4a) and compared to the results given by the quantum-corrected model (Fig. 4c). Substantial differences can be appreciated. Similarly, the calculation of the near-field within a classical or a quantum-corrected model produces profound differences in the spectra, reducing the field-enhancement of the antenna modes when the separation is smaller than ~3.5Å.

Most situations in optical nanoantennas involve nanometer-scale structures and distances where Coulomb interaction acts very effectively to tailor the antenna resonances. According to the results described above, to expose the quantum nature of the electrons collectively oscillating at each side of the gap requires accessing and controlling subnanometric distances. Experimentally, it is very challenging to reach the quantum limit through a direct optical fingerprint (colour) because this identification requires reaching separation distances below half a nanometer, thus exceeding the capabilities of most experimental optical techniques. However, by an exquisite control of separation distances, together with a simultaneous characterization of optics and transport properties, the Nanophotonics group lead by Prof. Jeremy J. Baumberg at University of Cambridge, U.K., has managed to reveal experimentally the quantum regime in tunneling plasmonics through a change of color of the cavity ⁴. Baumberg’s group managed to locate two AFM metallic tips that ended in spherical caps at subnanometric distance and horizontally aligned (schematics shown in Fig. 3) thanks to measurements of the capacitance of the cavity given by the force between the nanoobjects. The challenge was, as for so many other groups worldwide, to have simultaneous control of the conductance properties, the optical characterization (colour), and to exquisitely locate the massive (nanometric) tips at subnanometric distance in a controlled way. In a novel experiment that revealed the quantum regime in optical antennas for the first time, all these challenges were overcome [4]. The two tips are made to land at about 40 nm separation distance, and then approached together down to about 1 nm where a snap-to-contact situation is produced. A slow and controlled push of the tips together is manifested in the optical spectrum, acquired simultaneously during the whole approach, by using a dark-field microscopy set-up. The spectral trace of this situation, confirms that when the two massive gold tips reach about ~3.5Å of separation, the antenna resonance confined in the cavity starts being screened due to the quantum mechanical tunneling of electrons between the tips. Due to this quantum-mechanical effect, the optical response of the antenna gap (typically characterized by a red colour) is shifted suddenly to the blue, a clear chromatic fingerprint of the tunneling effect. In a metaphoric analog, the quantum touch between the particles, without physical touch, can be understood as a quantum kiss between the particles that changes the colour of the gap from red to blue.

About the author: Javier Aizpurua achieved his Ph. D. at the University of the Basque Country on the theory of Plasmon excitation by fast electron beams. After research positions at Chalmers University of Technology (Sweden) and NIST (USA), he worked at the Donostia International Physics Center DIPC as a research Fellow. He currently holds a position as a senior scientific researcher of the Spanish Council for Scientific Research (CSIC) at the Materials Physics Center in San Sebastián, Spain where he leads the research line on theory of Nanophotonics.