Why schools inflate grades
In 2012 the Nobel Memorial Prize in Economic Science was granted to two mathematicians, Lloyd Shapley and Alvin Roth, “for the theory of stable allocations and the practice of market design”. The market design in their theory was not exactly a market, at least, not the kind one usually calls that way. They are what economists call “matching games”. Examples are the assignment of doctors to hospitals, students to schools or organs for transplant to recipients. There are reasons not to treat these economic problems as regular markets or auctions. Schools sure want the applicants’ money, but they also have strong incentives to attract the best students, and simply letting candidates bid for admissions would not be efficient, as the future of the school may be compromised if its reputation for good quality is valued by prospective students. The case for the organs transplants has to do with the society finding repugnant its assignment by money. The rest of the matching games have also their own idiosyncrasies.
After the Nobel Prize in this area, the basic algorithms for solving the matching games in an efficient and stable manner were popularized, like the one in the seminal paper by Gale and Shapley (1962) 1. The interested reader, however, should know that there are many variants and complications to the problem. A matching can be done between two separate sets of individuals (like a heterosexual marriage game) or within one set (the homosexual marriage game), it may be one-to-one, one-to-many or many-to-many, all individuals in one group may have the same or different preferences regarding the individuals of the other group, there may be problems with externalities (I may be interested not only in my matching, but in the way others are matched), etc. Of special importance is the problem of individuals not revealing their true preferences if they are not publicly known, which is the question first studied by Roth (1982) 2.
In this article I will examine one of the latest advances on the field. In the particular problem of college assignment it is observed that high schools do not provide complete records of their students, and that colleges do not insist on having them, and that colleges do the same thing, with employers do not insisting either. For instance, schools can inflate grades: by giving A’s to most students they actually conceal necessary information to tell apart the average from the good and the good from the best. Why is that? This is the question Ostrovsky and Schwarch (2010) 3 try to answer.
A simple example shows the puzzle. Imagine that college positions are given values between 0 and 100, and that students’ abilities have also values between 0 and 100. Suppose further that both distributions are uniform. There is only one equilibrium in this situation: the best student goes to the best position, the second best student to the second best position and so on. Notice that no student can ask to change to a better position where he or she is preferred to the student that occupies it. Consider now that one school decides to conceal the grades of its students and that colleges know just its average value, then all the students will have and expected value of 50 and will be granted admissions around the positions with a value of 50 (it is assumed that one particular school is very small and that there will be enough such positions). By concealing the information the school offers no expected advantage to its students, as 50 is also the average position of a student of that school when complete information is provided.
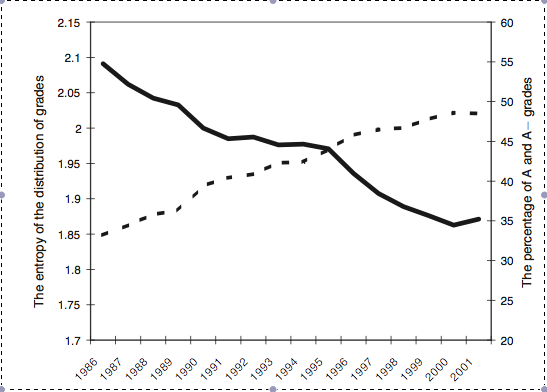
The dashed line shows the percentage of A- grades and A grades among all grades at Harvard. The solid line shows the entropy of the distribution of grades. If all students receive the same grade, no information is revealed and entropy is minimized. If a transcript structure is modified in a way that reduces the amount of information (e.g., students who had a C or a D grade can no longer be distinguished), entropy goes down. | Credit: Ostrovsky & Schwarz (2010)
Now consider the case that half of the schools (with half of the total students) have students with abilities uniformly distributed between 0 and 50 while the other half of the schools have students with abilities uniformly distributed between 0 and 100 (call these the higher than average schools). The population of students with abilities between 50 and 100 constitute one quarter of the student population, so they will occupy positions with values between 75 and 100 (with an average of (100+75)/2=87,5) while students with abilities between 0 and 50 will occupy positions between 0 and 75 (with an average of 75/2=37,5). The students of a higher than average school will have an average position of ½87,5+½37,5= 62,5.
But this cannot be an equilibrium situation, as one higher than average school can adopt the “no grade disclosure” and give every student the same transcript. The students of that school will have an expected ability of 50, which will given positions around 75, higher than the average 62,5 if they provide full information of their students!
So, if full revelation of information is not an equilibrium, what is it? It turns out that there is indeed an equilibrium in which some schools conceal some information about their students. The situation requires that schools conceal the information in a way such that the expected abilities of students from a distribution in which the expected ability of the students of a given school with its particular mix give the students access to a position that is of no lower value than the expected positions they would get if they were not mixed by the school (or if they were mixed in a different way).
The authors then show that an essentially unique amount of information is disclosed in all equilibria. They call this the balanced amount of information disclosure. From there, they can also show that other ways of concealing information are closely related to the one presented so far. In particular, schools are not the only actors in this market who can suppress information. By signing contracts early, students and employers can forgo the information about the students’ performance in the last few semesters. If these two possible ways of concealing information are present, there will be a trade off between their use in the equilibrium. If schools disclose the balanced amount of information, students and firms will not have incentives to contract earlier. However, if schools disclose more information, they will have the incentive to do it.
The work does not analyze the efficiency of the equilibrium, and the possible alternative matching mechanisms that will be the natural object of study if it turns out that it is not efficient, but sets the framework for continuing this line of research.
References
- Gale, G. and Shapley, L.S. 1962. College admissions and the stability of marriage. American Mathematical Monthly 69, 9-14. ↩
- Roth, A. 1892. The economics of matching: stability and incentives. Mathematics of Operations Research 7, 617-628. ↩
- Ostrovsky M. & Schwarz M. (2010). Information Disclosure and Unraveling in Matching Markets, American Economic Journal: Microeconomics, 2 (2) 34-63. DOI: 10.1257/mic.2.2.34 ↩
