Curling the path of a curling stone
Is there anyone that doesn’t know the sport of curling? Just in case: curling is a winter sport played indoors where two teams take turns sliding rocks on ice, trying to place them as close as possible to the button, a target area of four concentric rings placed about 30m away. One curler delivers the stone, while two sweepers use brooms to polish the ice path for the stone. It is one of the few sports to have mixed gender teams in official competitions.
As both teams take turns delivering the stones, there is a big tactical component on the game, apart from the necessary skill. The captain decides the weight (speed), line (direction) and turn (rotation) of the stone. There are three components because, in order to dodge the stones that are already in play, the curler might curve the path substantially by applying a small rotation to the stone (turn) before releasing it. Also, sweepers might increase the curl even further by brooming the ice in a specific way. However, the friction coefficient of polished marble against ice is extremely low, so how does a rather small rotation of the stone generate such a big curvature on its path?
Once the stone is delivered no one must touch it, so the only interaction is between stone and ice; this is, the force necessary for achieving the curled path must come from the tribological properties of the contact patch. Some years ago, Shegelski et al 1 proposed a mechanism that would allow this behaviour: the necessary momentum would be achieved by having different friction coefficient between the leading and rear part of the stone. This way, the rear with increased friction would generate a higher lateral force than the leading half with less friction, pushing the stone sidewise, as in Figure 1. You can actually find this explanation in several internet sites dedicated to curling.
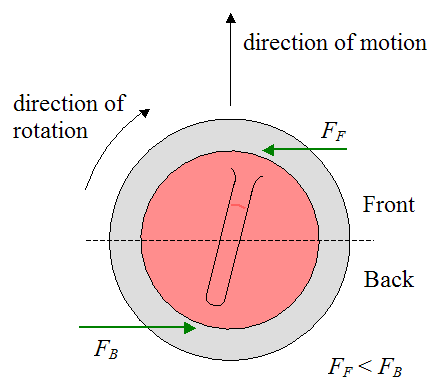
But it seems curling stones are not that simple. The experience of curlers and the experimental evidence shows that the curl will be rather independent of the rotation of the stone: it is always around one meter deflection. And with the aforementioned mechanism, the total deflection should be proportional to the rotation speed, not independent. There have been regular studies unsuccessfully trying to either modify the existing model or creating a new one that explains this phenomenon, and now Nyberg et al 2 have finally found a mechanism that allows a lateral drift independent of the rotational speed. But in order to explain it we need to introduce some technical aspects of curling first: ice and stone topography.
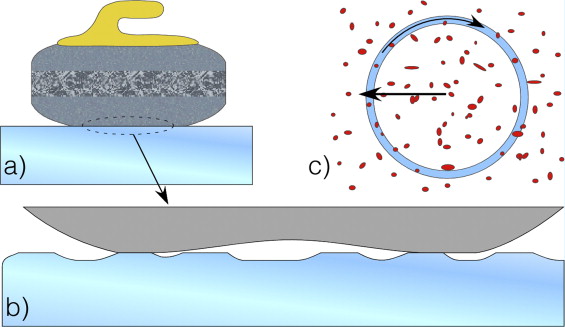
First of all, the ice surface must be as smooth as possible, so the stone is not deviated from the intended path. But having an extremely smooth surface will make the stone stick to the ice, so the lane is sprayed with water before the game starts. When drops contact the ice they are immediately frozen, leaving a surface full of ice pebbles that will allow the stones to avoid full contact of the running band. After the first delivers these pebbles will be worn off, so in order to avoid different properties in different stages of the game, the pebbles are cut off before the match starts.
Then there is the curling stone. It’s a polished marble stone with a curved hollow base; this is, the contact surface is a ring, as can be seen in Figure 2. However, in order to have some traction between the stone and the ice, and thus allow delivering it with a reasonable effort, the running band is intentionally scratched.
When a stone is delivered with some turn, all the contact patches (the highest peaks in the not-so-smooth running band) will scratch the surface of the ice in a way such as figure 3, where the contact points in the front will create some paths that will later interact with the contact points in the rear half: for a clockwise turn, right handed forces will appear when the rear contact points encounter the scratch generated by the front contact points. This mechanism would generate left handed forces for a counter-clockwise turn.
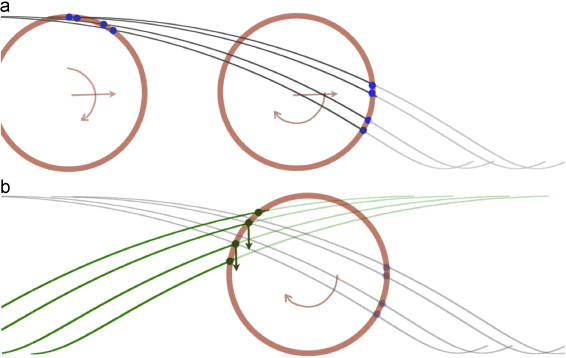
In order to test their theory, the authors pre-scratched the ice diagonally, and curling stones with no turn deviated from the straight path; when having several differentiated zones with scratches in opposite directions, the stones performed a zig-zag movement; and when using a stone with a smooth polished base, the path was not curved at all for both clean and pre-scratched ice. This demonstrates the importance of both the scratches and the topology of the sliding ring on the stone, which previous authors had never considered in their models.
But why is this mechanism not affected by the rotational speed of the stone? According to the authors, there are three factors that act when speed is changed: i) the number of scratches crossed for a given time increases linearly, ii) the sideward force on a surface tip seems independent of the crossing angle, and thus the rotating speed, and iii) the sliding distance needed for a tip to enter the wall after a scratch is inversely proportional to the rotating speed. The combination of these three factors would allow a lateral force almost independent from the turn of the stone.
First historical curling rocks date from year 1511 from Scotland, being a very popular winter sport between the 16th and 19th centuries. Did these predecessors turn their stones so they could curl their paths? Probably not, as stones were not manufactured back then, but stones picked from rivers. In modern times, it became an official Winter Olympics sport in 1998, with the curl of the stone already embedded in the DNA of the sport. When was the scratching of the running band introduced? Was it intentional so that it would allow the curving of the path? We might not know these answers, but at least we know how thecurling of the curling stone works.
References
- M.R.A. Shegelski, R. Niebergall, M.A. Walton, The motion of a curling rock, Canadian Journal of Physics 74 (1996) 663–670 ↩
- Nyberg H., Alfredson S., Hogmark S. & Jacobson S. (2013). The asymmetrical friction mechanism that puts the curl in the curling stone, Wear, 301 (1-2) 583-589. DOI: 10.1016/j.wear.2013.01.051 ↩

2 comments
[…] Jada jolastutako harriak saihesteko, curling-jaurtitzaileak ibilbidea nabarmenki makurtu edo kurbatu dezake harria askatu aurretik biraketa txiki bat eraginez. Pista garbitzaileek ere errotazioa handitu dezakete modu jakin baten izotza eskuilatuz. Baina izotzaren kontra leundutako harri baten marruskadura-koefizientea oso txikia da […]
[…] mappingignorance.org […]