Forming bubbles in liquid light

Authors:

Ángel Paredes Galán got a Ph. D. in Particle Physics from the University of Santiago de Compostela in 2004. After postdoctoral stays at École Polytechnique (France), University of Utrecht (the Netherlands) and University of Barcelona (Spain), he joined the Optics group at University of Vigo as a Ramon y Cajal fellow.

David Feijoo Pérez is a predoctoral student at the Optics group in Universidade de Vigo. He studied Physics at this university, finishing the degree in 2011. In 2012 he finished the master’s programme in Photonics and Laser Technologies.

Humberto Michinel Álvarez. Phd. in Applied Physics (optics) from University of Santiago de Compostela in 1996. Full professor of optics at the University of Vigo in Ourense, Spain. Vice-president of the International Commission for Optics (ICO). Prof. Michinel is the director of the MSc program “Photonics and Laser Technologies”.

For many centuries, the passage of light through matter was regarded as that of a wave in a fixed medium characterized by a refractive index (n), which may depend on the frequency. This description is consistent with plenty of phenomena, including diffraction, interference, refraction, dispersion or polarization, associated to distinguished names of the history of Physics such as Huygens, Newton or Fresnel. After the advent of lasers in the early sixties, it was soon proven that intense light can alter the optical properties of a medium and thus affect its own propagation. This was the outset of the fascinating discipline of nonlinear optics in which, for instance, light can act as a lens for itself or can even generate new frequencies while propagating. These phenomena have found numerous practical applications and, nowadays, are essential in many photonic devices.

Depending on the material, the refractive index varies with light intensity in different forms. Taking this effect into account, the wave equation becomes nonlinear, typically leading to an enormous wealth of qualitatively distinct behaviors. We are interested here in the particular expression n = n₀+n₂I-n₄I², where n₀, n₂, n₄are positive constants and I is the intensity of light (energy traversing the unit of area in the unit of time). After some manipulations, this setting leads to the so-called cubic-quintic nonlinear Schrödinger equation:

i ∂_z ψ = – (∂_x² +∂_y²)ψ – (|ψ|²-|ψ|⁴) ψ (1)

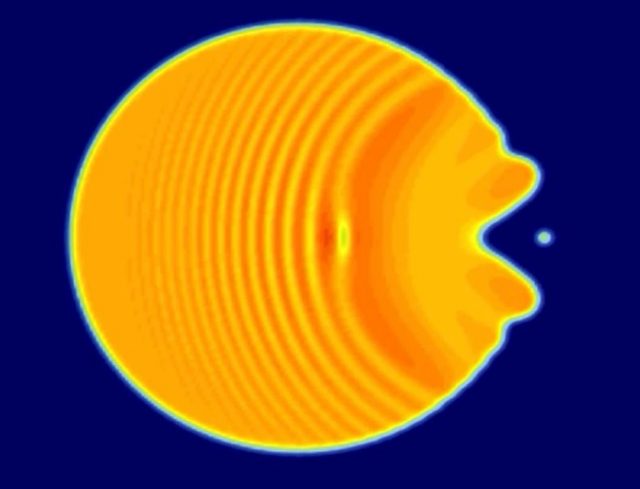
Remarkably, solutions of this equation in certain regimes share many properties with usual liquids ¹. We could speak of droplet formation, surface tension or capillarity, but maybe the simplest way to convince oneself is by watching a video in which the collision of a light droplet with a barrier is simulated numerically solving equation (1). We plot the evolution of |ψ|², which is proportional to the intensity.

Different materials have nonlinear refractive indices of this sort, but typically accompanied by absorption coefficients which have hindered the clear observation of the mentioned properties. But recently, these difficulties have been overcome and the first neat realization of the liquid of light has been reported in ², where a suitable coherent atomic medium was utilized to study the propagation of a laser beam. These results are an obvious motivation for further theoretical studies of equation (1).

Despite its limitations, analogies as that of (1) with a liquid are certainly appealing and helpful in understanding complex phenomena. Moreover, they are useful to formulate new questions. For instance, can bubbles exist in the liquid of light? If so, how can they be formed? This was the starting point of our recent work ³ which, incidentally, was chosen for the cover of its issue of Physical Review Letters.

The answer to the first question is yes. It comes to no surprise, since the result is similar to what happens with other nonlinear potentials in analogue Schrödinger equations. Those bubbles are only stable if they move in a certain range of velocities – for velocity here we mean displacement in the transverse direction or angle of propagation. Their technical name is “rarefaction pulses”. At lower velocities, one finds that the stable solutions are pairs of vortices rotating in opposite directions.

But a distinct feature of cubic-quintic media is that, apart from those dark spots, there are also “bright solitons”, which are, say, liquid droplets of different sizes. If we make two of these droplets collide, it is conceivable that destructive interference (you cannot do this with water!) creates a void in the large one which may evolve into a stable moving bubble. This is confirmed by numerical simulation. Remarkably, when the dark blob reaches the other end, it is converted in a bright soliton again. You can watch the process in the following animation:

It is worth mentioning that bright-dark-bright conversions are not unusual in nonlinear equations, especially in one-dimensional situations, see e.g. ⁴. In contrast, we are dealing here with a two-dimensional case.

The term “cavitation” is used for the formation of vapor cavities in liquids. Following the analogy, and since the coherence of the beams is essential for interference, the process just explained can be suitably tagged as “coherent cavitation”. In order to stress the importance of coherence and interference, notice that the collision develops diverse features depending on the relative phases of the light droplets. Those relative phases are the only difference between the previous simulation and any of the following two. In the first one, the droplets coalesce. In the second one, they bounce against each other and a faint bubble appears too.

In fact, notice that these disparities can turn out to be useful if this set-up is realized in the lab. Apart from being a handy probe for the parameters defining the beams themselves, one can think for instance of using the light droplets as filters letting pass only particular velocities and phases.

Nonlinear systems are exciting and full and surprises. They are an alluring subject of research from both the theoretical and the experimental sides. The different processes found by numerical investigations in [3] and described above may eventually be instrumental in the control of light by light. And there is no doubt that there are still many questions waiting to be asked and answered.