Isotope Anomalies in Superconductors and the Pairing Mechanism

When in April 1911 Kamerlingh Onnes and coworkers measured that the electrical resistivity of mercury suddenly vanished at 4.2K, they could not believe it. They repeated the experiment several times looking for a short circuit that could explain the weird observation. But any experimental set up was leading to the same result. They had discovered superconductivity, one of the most spectacular and unexpected phenomena in solid state physics.

Superconductivity is simply extraordinary, and it demonstrates the complexity hidden in condensed matter. Even if electrons repel each other, when a solid becomes a superconductor below the critical temperature Tc pairs of electrons are formed, the so-called Cooper pairs. Electrons pair as a consequence of an effective attractive interaction between them. The attractive interaction is however so weak that it can hold the Cooper pairs only at very low temperatures, below Tc. Above Tc, the Cooper pairs are decoupled and the metal recovers its finite electrical conductivity.

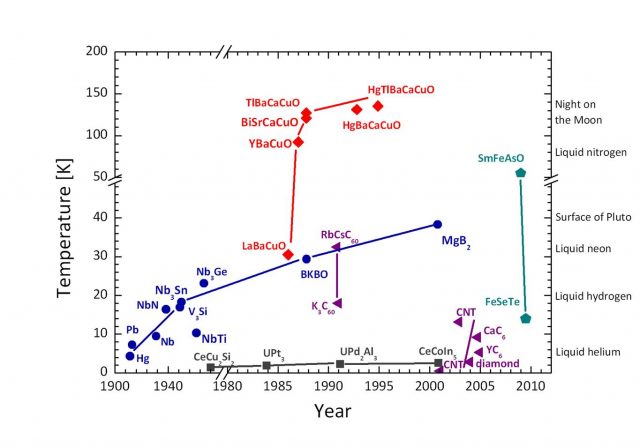
As shown in figure 1 there are three main families of superconductors: normal metals, which have rather low Tc’s, and the high-Tc cuprates and pnictides. The recent discovery of the pnictide family strengthens the hopes of finding a room temperature superconductor. If one day we had a room temperature superconductor, we would be able to transport electricity with no losses, build levitating fast trains with no risk of derailment, and create strong magnets for many applications without the need of extreme cooling.

Understanding the pairing mechanism is crucial to find superconductors with higher values of Tc. Unfortunately, among the above mentioned three families, we only know how Cooper pairs are formed in normal metals. The origin is the interaction of the electrons with the phonons, the quanta of atomic vibrations. The pairing mechanism in cuprates and pnictides remains a mystery and one of the biggest challenges for physicists.

Understanding how Tc scales with the mass of the atoms in the superconducting compound is crucial to unveil the pairing mechanism. Indeed, when it was proposed in 1957, the phonon based explanation of Bardeen, Cooper and Schrieffer (BCS) ¹ was widely accepted partly because it could rigorously explain how Tcscaled with the atom mass M.In the known superconductors at the time Tc scaled with the mass as M^–α, where α, the isotope coefficient, was around 0.5. The BCS theory could correctly explain this behavior since it predicts that

Tc ∝ ω Exp(-1/λ), (1)

where ω is an average phonon frequency and λ is the electron-phonon coupling constant. In fact, considering that generally λ is independent of the atom mass M and ω scales as M^–0.5, in the BCS theory Tc scales as M^–0.5 as well, in agreement with experiments.

The story is different in high-Tc superconductors, which were discovered later. The isotope coefficient almost vanishes in cuprates ² and it is rather controversial in pnictides, where very different positive and even slightly negative values of αhave been reported³⁴. The departure of α from the expected 0.5 value is a clear fingerprint of an unconventional coupling mechanism not driven by the electron-phonon interaction, evidencing that the BCS theory cannot explain the pairing.

However, the most anomalous isotope effect ever measured does not belong to the family of cuprates or pnictides, but to the superconducting palladium hydrides ⁵. PdH has a superconducting temperature of 8K. Substituting hydrogen by the heavier deuterium leads to a higher value of 10K, making the isotope coefficient negative, approximately -0.3. This is in stark contrast with the α=0.5 value expected in electron-phonon BCS superconductors. Does this mean that palladium hydrides are unconventional superconductors like the cuprates and pnictides? Do they form a different family? How can this be possible if palladium hydrides are supposed to be normal metals?

It has been recently shown making use of first-principles calculations that the origin of the strong isotope anomaly in palladium hydrides is the huge anharmonic effects that drive the atomic vibrations in the system [6]. Remarkably, when anharmonic effects are included in the description of the phonons, the electron-phonon mechanism explains the observed Tc values in the different hydrides, correctly predicting the -0.3 value of the isotope coefficient.

The reason is that in the BCS theory α is exactly 0.5 if and only if the atomic vibrations are harmonic, that is, if the force felt by an atom when displaced from its equilibrium position is linear with the displacement. In this case, ω scales as M^–0.5 making the electron-phonon coupling constant λ mass independent. In most metals atoms vibrate close to their equilibrium positions and, thus, the harmonic approximation is valid so that α=0.5. However, in palladium hydrides the harmonic approximation completely breaks down as hydrogen atoms vibrate with a very large amplitude around their equilibrium positions. As a consequence, ω does not scale anymore as M^–0.5 and λ becomes mass dependent. Indeed, the anharmonic electron-phonon coupling constant is strongly suppressed with respect to the harmonic λ. Considering that hydrogen is lighter than deuterium, it feels the potential farther away from equilibrium. Consequently, the anharmonic effects are larger the lighter the isotope, and λ is more strongly suppressed in PdH than in PdD. Since, as deduced from Eq. (1), Tc increases with λ, the differences in the electron-phonon coupling constant explain why Tc increases with the isotope mass.

As it was stressed throughout, understanding the mass dependence of Tc is crucial to figure out the coupling mechanism in superconductors. The first-principles calculations presented in Ref. ⁶ have evidenced that anharmonic effects can indeed induce huge anomalies in the behavior of the critical temperature with respect to the atomic mass. These findings open new perspectives in the interpretation of isotope effects in superconductors.