The whip of the electric jet
Everyone has heard the sound of the crack of a whip, at least in movies or TV serials like “El Zorro: The man with the whip” (1954). A shock wave is created by the supersonic motion of the tip of the whip in the air 1. Whipping is a typical fluid instability of an accelerating fluid jet in an electric field 2. Fundamental research on its structure and its properties, and its use in industrial applications, have been precluded by its chaotic behavior. Alberto Fernández-Nieves (Georgia Institute of Technology, Atlanta, GA, USA) and colleagues 3 have discovered that when the longest characteristic time scale of the problem is that of the surrounding liquid, the whipping structure is steady and helicoidal, instead of chaotic. Under this condition, a detailed analysis of steady-state whipping has been attained using microfluidics experiments.
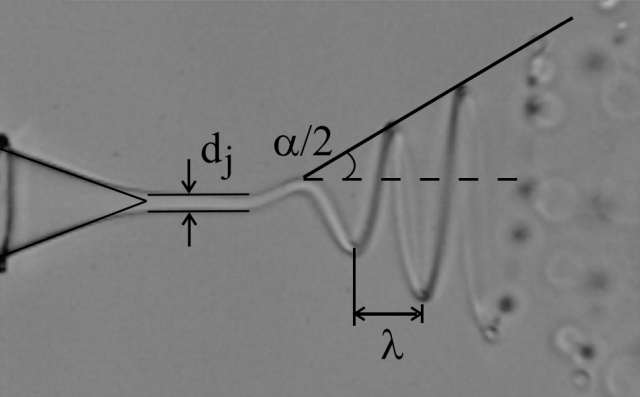
Electrospinning is a method for making coaxial liquid jets composed by two immiscible, conducting liquids thanks to electrohydrodynamical forces [5]. Both liquids are injected using two coaxial needles subject to an electric potential difference. The electric field causes the meniscus to adopt a conical shape (the so-called Taylor cone) resulting from the balance between electric and surface tension stresses. An electrified, thin, coaxial liquid jet appears in the apex of the cone4, whose diameter is independent of that of the needles, so it is possible to make micro- and, even, nanometric jets.
The cone–jet structure is stable for certain values of the applied voltage and liquid flow rate. However, Rayleigh–Plateau axisymmetric instabilities can break the jet and result in droplet formation, a process with industrial potential in producing micro- and nanoparticles with either simple or core-shell structure (micro- and nanocapsules for drug delivery systems, particles and bubbles for biomedical engineering applications, coaxial nanofibers, hollow nanofibers, and other nanomaterials) 56. But there also are nonaxisymmetrical instabilities due to the electrostatic repulsion between bent and straight parts of the jets. This whipping instability is difficult to control due to its chaotic character (Movie 1).
Movie 1. Chaotic whipping in electrified liquid jet. | Credit: J. Guerrero et al. (2014)
Fernández-Nieves and colleagues [3] used a moderately conducting liquid surrounded by a coflowing liquid to generate a steady-state whipping structure (Figure 1). Its shape is helicoidal due to the electrostatic repulsion between the fluid elements of the jet in the whipping region. Numerical simulations show that this conical helix structure is the natural configuration of the electrified jet even in the absence of a coflowing liquid, but it is required for the stability of the whipping structure.
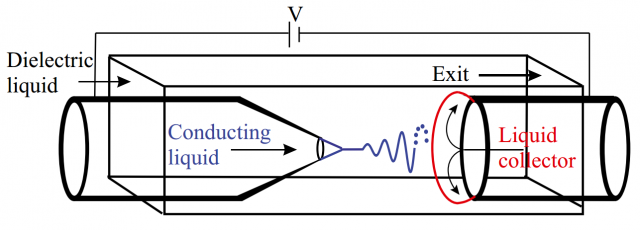
Figure 2 shows the schematics of the experiment. The whipping conducting liquid is ethylene glycol, with electrical conductivity 10−4 S/m (Siemens per meter) and viscosity 17 mPa·s (millipascal-second). This liquid is injected by using a capillary into a dielectric liquid, polydimethylsiloxane oil, with viscosity 1.5 mPa·s. To collect the jet whipping structure a A third, conducting liquid is used. A high voltage is applied between the inner and third liquids to obtain a steady-state whipping structure. In Figure 1 and Movie 2, with a voltage of 1,800 V (volts) and a flow rate of 80 μL/h (microliters per hour), results in α = (46.29 ± 0.12)°, λ = (25.26 ± 0.07) μm, and jet diameter dj = λ/4; the whipping velocity, i.e., the phase velocity of the wave, is v=λ/T with T = (192.3 ± 0.1) μs.
Movie 2. Steady-state whipping in electrified liquid jet (recorded at 26,000 fps (frames per second) and reproduced at 6 fps). | Credit: J. Guerrero et al. (2014)
In order to understand the steady-state whipping structure a mathematical one-dimensional model has been developed and solved by using a numerical method. The model does not consider the presence of an outer fluid medium, and assumes that the jet is slender and Cosserat’s rod theory is applicable. The readers interested in the technical details must consult Ref. [3]. There is a good agreement between the model and the experiment. The model suggests that the dominant force in the whipping instability is the electrostatic self-repulsion of the jet. Moreover, the whipping structure is stable (chaotic) when the longest characteristic time scale is that of the outer (inner) liquid.
In summary, the conditions for steady-state whipping in charged liquid jets have been determined. The results of this fundamental research could be used in electrospinning to make polymer fibers with a helicoidal structure. Obviously, further studies are required before the whipping could be exploited in industrial applications.
References
- Alain Goriely and Tyler McMillen, “Shape of a Cracking Whip,” Physical Review Letters 88: 244301, 2002. DOI: 10.1103/PhysRevLett.88.244301 ↩
- Y. M. Shin, M. M. Hohman, M. P. Brenner, and G. C. Rutledge, “Electrospinning: A whipping fluid jet generates submicron polymer fibers,” Applied Physics Letters 78: 1149–1151, 2001. DOI: 10.1063/1.1345798 ↩
- Guerrero J., V. R. Gundabala, M. Perez-Saborid & A. Fernandez-Nieves (2014). Whipping of electrified liquid jets, Proceedings of the National Academy of Sciences, 111 (38) 13763-13767. DOI: http://dx.doi.org/10.1073/pnas.1411698111 ↩
- J. Fernández de la Mora and I. G. Loscertales, “The current emitted by highly conducting Taylor cones,” Journal of Fluid Mechanics 260: 155–184, 1994. DOI: 10.1017/S0022112094003472 ↩
- I. G. Loscertales, A. Barrero, I. Guerrero, R. Cortijo, M. Marquez, and A. M. Gañán-Calvo, “Micro/Nano Encapsulation via Electrified Coaxial Liquid Jets,” Science 295: 1695–1698, 2002. DOI: 10.1126/science.1067595 ↩
- Antonio Barrero and Ignacio G. Loscertales, “Micro- and Nanoparticles via Capillary Flows,” Annual Review of Fluid Mechanics 39: 89–106, 2007. DOI: 10.1146/annurev.fluid.39.050905.110245 ↩
3 comments
[…] disfrutarán con Francisco R. Villatoro, “The whip of the electric jet,” Mapping Ignorance, 29 Sep 2014. Incluye dos vídeos youtube y se basa en el artículo técnico Guerrero J., V. […]
[…] Zinemak zartailu baten krakadarekin ohitu gaitu. Baina ez genuen sumatzen eskala mikrometrikoan fluidoak, eremu elektriko baten eraginez, zartailuak bezala portatzen direla. Francisco R. Villatorok azaltzen digu The wip of the electric jet-en. […]
Hola Francis,
He pillado el artículo tarde. Aunque sea para tus archivos y barriendo para casa, este artículo es muy relevante y concluimos que aunque la autorepulsión amplifica la inestabilidad del chorro, la perturbación inicial parece ser puramente hidrodinámica.
Y también éste video!
Un Saludo
Alvaro