The necessary connection between electric and magnetic fields

We finished our last article saying that it is one thing to accept this newly stated connection between electric and magnetic fields; but it is a little bit harder, and more interesting, to understand the physical necessity for such a connection. We will try to explain this necessity now avoiding the use of mathematics, step by step. Some of the concepts we will explore are quite common in condensed matter physics and are widely used by DIPC researchers, for example.

An uncharged insulator (such as glass, wood, paper, or rubber) contains equal amounts of negative and positive charges. In the normal state, these charges are distributed evenly. Thus, the net charge is zero in every region of the material. But when the insulator is placed in an electric field, these charges are subjected to electrical forces. The positive charges are pushed in one direction, the negative in the opposite direction. Unlike the charges in a conductor, the charges in an insulating material are not free to move far through the material. The charges can be displaced only a small distance before restoring forces in the insulator balance the force of the electric field. If the strength of the field is increased, the charges will be displaced further. But the changing displacement of charges that accompanies a changing electric field in an insulator briefly forms a current. Maxwell called this current a displacement current. He assumed that this momentary displacement current in an insulator surrounds itself with a magnetic field just as a conduction current of the same magnitude does.

In an insulator, the displacement current is defined as the rate at which the charge displacement changes. This rate is directly proportional to the rate at which the electric field is changing in time. Thus, the magnetic field that circles the displacement current can be considered a consequence of the time-varying electric field. Maxwell assumed that this model, developed for matter, also applies to space free of matter (though at first glance this may seem absurd).

Therefore, under all circumstances, as noted above, an electric field that is changing with time surrounds itself with a magnetic field. Previously, it was thought that the only current that produced a magnetic field was the current in a conductor. Now Maxwell predicted that a magnetic field would also arise from a changing electric field, even in empty space. Unfortunately, this field was very small in comparison to the magnetic field produced by the current in the conductors of the apparatus. So it was not at that time possible to measure it directly. But Maxwell predicted consequences that soon could be tested.

According to Maxwell’s theory, then, the two basic principles of electromagnetism should be expanded by adding a third principle:

1. An electric current in a conductor produces magnetic lines of force that circle the conductor.

2. When a conductor moves across externally set-up magnetic lines of force, a current is induced in the conductor.

3. A changing electric field in space produces a magnetic field.

For instance, consider a pair of conducting plates connected to a source of current. Charges are moved onto or away from plates through the conductors connecting them to the source. Thus, the strength of the electric field in the space between the plates changes with time. This changing electric field produces a magnetic field.

An additional principle, known before Maxwell, assumed new significance in Maxwell’s work because it is so symmetrical to principle 3:

4. A changing magnetic field in space produces an electric field.

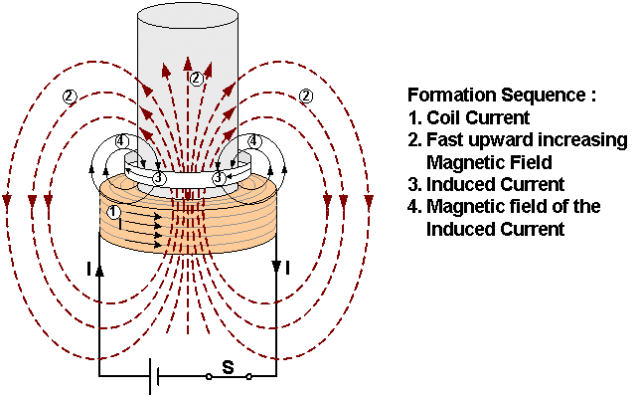
In this case we can consider the changing magnetic field produced by temporarily increasing the current in an electromagnet. This changing magnetic field induces an electric field in the region around the magnet. If a conductor happens to be lined up in the direction of the induced electric field, the free charges in the conductor will move under the field’s influence. Thus, a current in the direction of the induced field will arise in the conductor. This electromagnetic induction had been discovered experimentally by Faraday.

Maxwell’s theory, involving the total set of relations between electric and magnetic fields in space, was not at once directly testable. When the test finally came, it concerned his prediction of the existence of waves travelling as interrelating electric and magnetic fields, that is, as electromagnetic waves.

References:

Asimov, I. (1993) New Guide To Science Penguin Press Science

Cassidy, D. et al (2002) Understanding Physics Springer Verlag New York

Author: César Tomé López is a science writer and the editor of Mapping Ignorance.