How water molecules penetrate salt crystals, seen one at a time.

Imagine that you enter a room full of a poisonous gas wearing a mask that is not good enough to prevent the gas reaching your lungs and killing you. The mask is not good enough because it would allow the gas to diffuse through the fabric it is made of, eventually reaching your nose and mouth. Still the mask will give you some time inside the room because it will make more difficult for the gas to get inside you. What you may not imagine is that the time of protection that this kind of mask would provide is determined by a statistical equation first derived by no other than Albert Einstein.

He envisioned a gas particle to move a distance before colliding with another particle. After this collision, memory of the initial direction of motion is lost and the particle is free to move in the same or a new direction until the next collision occurs. This conceptual picture of particle motion is mathematically described by the statistical approach to diffusion. In the statistical approach particle diffusion is also modeled as a series of discrete displacements or steps, with the direction of one step being uncorrelated with that of the previous step. That is, once the particle has taken a step, the direction of the next step is random. A series of such steps is referred to as a random walk. The result is a net displacement from one part of the system (of high concentration, in our example the room) to another part of the system (of low concentration, your nostrils). How long does it take any one particle to move a certain distance, given this random-walk description of its motion? That is, can we determine the net displacement of a gas particle?

The answers to these questions are the topic of one of Einstein’s seminal manuscripts that were published during his annus mirabilis, 1905. (Other topics include a rationalization of the photoelectric effect in terms of Planck’s quantum hypothesis, for which he received the Nobel prize in 1921, and special relativity). In trying to understand the phenomenon called Brownian motion, Einstein applied kinetic theory and determined an expression for the average displacement of a particle due to interparticle collisions and mean free paths.

For the average of the square (in order to avoid plus and minus displacements cancelling each other) of the one-dimensional displacement, Einstein derived an expression for the one-dimensional diffusion equation known today as the Einstein-Smoluchowski equation. Marian Smoluchowski was a Polish physicist who also considered the theoretical basis of Brownian motion independently of Einstein in 1906.

The Einstein–Smoluchowski equation is the central connection between the microscopic details of particle motion and the macroscopic parameters relating to diffusion (for example, the diffusion coefficient and, through the Stokes–Einstein relation, the viscosity).

This equation finds application in lots of interesting systems. A fundamental one is water at surfaces, specifically water-salt systems. Of these the water-common salt, sodium chloride, interaction is particularly important due to its crucial role in biophysics, environmental physics, even in astrochemistry and planetary science.

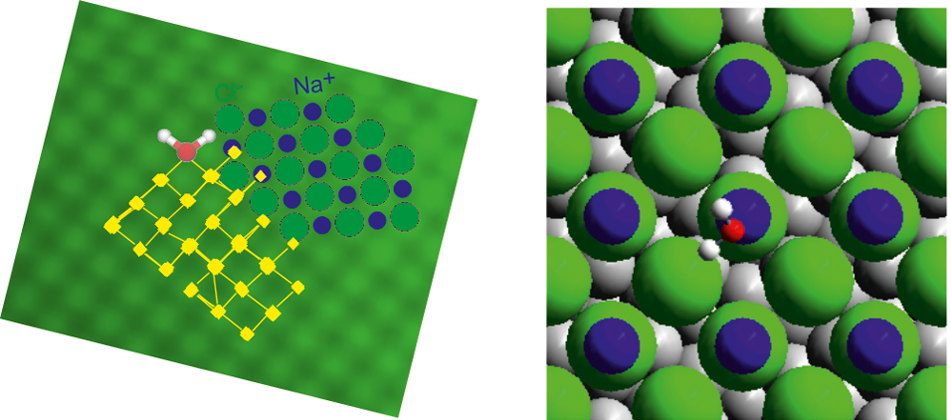
New techniques allow the experimental study of individual water molecules (what would suit the Machian-positivistic worldview of Einstein back in 1905). Now, a group of researchers, that includes Pepa Cabrera-Sanfelix from DIPC, has studied experimentally¹ for the first time the mechanism of water difussion on sodium chloride at the single molecule level. And yes, they have used the Einstein-Smoluchowski equation and determined the mechanism.

They investigate the diffusion of the deuterated version of water (D₂O) on bilayer sodium chloride islands on silver, at low temperatures (around -225 ºC), using scanning tunnelling microscopy (STM). This technique allows them to follow the motion of individual water molecules on sodium chloride by imaging the same spot of the surface repeatedly.

The results imply that the movement is truly random, thus the Einstein-Smoluchowski equation for two dimensions can be used to determine the water molecules diffusivity. From this they can calculate the energies implied.

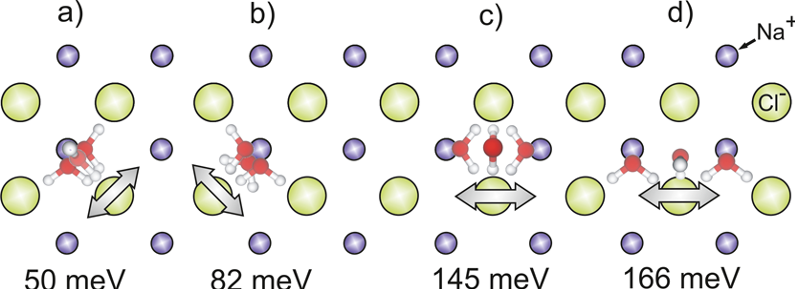
Theoretically there are six different diffusion processes possible. Of the only four that could apply here, none of them alone fits completely with the experimental results. Therefore, the researchers conclude the mechanism should be one of consecutive steps: one, called O-flip (c in Figure 2), where the oxygen atom of the water rotates 180 around the axis formed by its two H-bonds, thus keeping the H-bonds pointing to the same chloride ions; the other an in-cell motion (a, b in Figure 2) that involves the breaking of one or both of the weaker H-Cl bonds.

A question that may arise is whether this system of a bilayer of sodium chloride on a silver base is representative of sodium chloride in other systems. The researchers also investigate this question and find that the electronic bulk properties of sodium chloride are already reached at bilayer thickness, but the underlying metal still influences molecules adsorbed on it.

This work shows that layer thickness can be used to influence molecules, their diffusion and consequently their reaction kinetics.

Author: César Tomé López is a science writer and the editor of Mapping Ignorance.