Controlling dispersion forces with light
It is likely that you have read somewhere that gravity is much weaker than the electromagnetic interaction. And it is true: for the electron and the proton gravity is 39 orders of magnitude weaker. Still what governs the movement of moons, planets, stars and galaxies is gravity; even the existence of dark matter is deduced from its gravitational effect. The moral is that weak interactions are important.
In condensed matter some weak interactions exist that are extremely important for the behaviour of matter as we know it. The way proteins or blood cells, or milk, or paint, or bromine, behave depends on the weak van der Waals-London forces or, in general, dispersion forces. To control them on demand would be a major feat. This is what geckos do.

Dispersion forces are attractive forces between atoms and molecules but are much weaker than valence bonds; they are inversely proportional to the seventh power of the distance between the atoms or molecules (recall that in the Coulomb interaction the inverse proportionality is to the square of the distance).
These forces are responsible for the non-ideal behaviour of real gases, the lattice energy of molecular crystals and what makes that, even though they share the external electronic configuration, fluorine and chlorine are gases, whereas bromine is a liquid and iodine a solid at room temperature.
Dispersion forces arise from the fact that electrons show a collective behaviour, as a gas, in atoms and molecules. Actually the bigger the atom or the molecule, with increased shielding of the electrostatic effect of the nuclei, the more intense is the dispersion forces effect, hence the state of the halogens at room temperature.
Three factors account for dispersion forces:
-
dipole/dipole interactions, i.e., electrostatic interactions between molecules with permanent dipole moments.
-
Dipole/induced-dipole interactions, in which a dipole of one molecule polarizes a neighbouring molecule
-
arising small instantaneous dipoles in atoms
It was Fritz London in 1930 who gave a quantitative theory in terms of quantum mechanics of the forces that J.D. Van der Waals had described. He found, for example, that if the molecules are some 10 nanometres or more apart then relativistic effects would change the variation of the force from the inverse of the seventh power to the inverse of the eighth power. This change has been observed in colloids.
Controlling dispersion forces in colloids is most important. We find colloids almost everywhere in our daily life: in biological fluids, foodstuffs (dairy, creams, emulsions) or industrial suspensions (pharmaceuticals, slurries, paints or inks). Colloids have also been shown to be extremely well suited for the study of phenomena such as crystallization, the glass transition, fractal aggregation and solid–liquid coexistence. Still, current methods used to control dispersion forces in colloids have some serious issues: they alter the colloids themselves in different ways, or are slow or do not affect all the sample with the same intensity.
Now a group of researchers from IFIMAC-UAM, the University of Fribourg and DIPC present1 in Nature Communications a method to control dispersion forces in small particles using random laser lights.
The team introduce a new concept, that of random-light-field induced forces. These forces are a tool to control, no matter what the position of the particle may be at any time, the interactions between small particles in two or three dimensions with tunable strength and range.
The researchers show theoretically that, choosing the right colours and intensity, artificially generated random fields can provide an overall control of the interactions. Actually, they predict that the interactions between semiconductor particles with relatively high refractive index can be tuned from attractive to strongly repulsive.
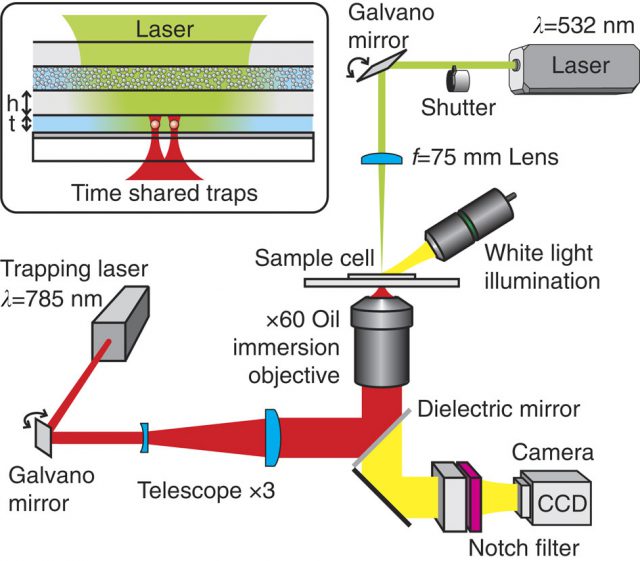
A turbid scattering layer at the entrance of the cell creates a random field distribution inside a light-filled cavity. From the opposite side, the sample cell is illuminated with a tightly focused near-infrared laser creating a set of two timeshared optical traps. Both laser beams can be steered by galvano mirrors. A white light source is employed for the broadband illumination of the cell,
allowing the tracking of the particles by video microscopy. Different filters are used to spectrally isolate the different optical paths. The interaction potential between the two trapped spheres is obtained by monitoring the thermal Brownian motion inside the optical traps with a digital camera (CCD). The inset shows an enlarged view of the sample cell: Two micron sized colloidal particles suspended in water are trapped in the centre of a water-filled layer. The water layer and the turbid layer are separated by a glass wall. The dichroic mirror at the bottom of the clear layer reflects 499% of the incoming light leading to multiple reflections inside the cavity. | Credit: Brügger et al (2015)
As a proof of principle, they make an experiment with two micron size dielectric particles using two high-intensity monochromatic lasers, a green one and a near infrared one (see Figure 2). A scattering layer at the entrance generates the random field distribution. They find that the behaviour is as predicted and that random-light-field induced forces act instantly on time scales of Brownian motion.
This result hints to the possibility that this method could be useful to anneal defects in periodic structures such as photonic crystals, to increase the effective temperature by optically shaking particles or to stabilize non-equilibrium phases such as supercooled liquids and, in general, to control the self-assembly and phase behaviour of colloidal particle assemblies on nano- and mesoscopic length scales. Even more importantly, it opens a pathway for a new field of fundamental research on isotropic optical forces.
Author: César Tomé López is a science writer and the editor of Mapping Ignorance.
References
- Georges Brügger, Luis S. Froufe-Pérez, Frank Scheffold, & Juan José Sáenz (2015) Controlling dispersion forces between small particles with artificially created random light fields Nat. Comm. DOI: 10.1038/ncomms8460 ↩