The van der Waals contribution to the mystery of the gas-metal interaction

We are all familiar with the equation of ideal gases: PV = nRT. To deduce this equation, an ideal model of the gas is considered. In this model, gases are composed of particles so tiny compared to the volume of the gas that they can be considered zero-volume points in space, and there are no interactions, attractive or repulsive, between the individual gas particles. However, real gases ultimately have behaviours due to the facts that gas atoms and molecules do have a size, and there is some interaction between the gas particles, which can range from minimal to very large. In considering the state variables of a gas, the volume of the gas particles should have an effect on the volume V of the gas. The interactions between gas particles would have an effect on the pressure P of the gas. Perhaps a better equation of state for a gas should take these effects into account.

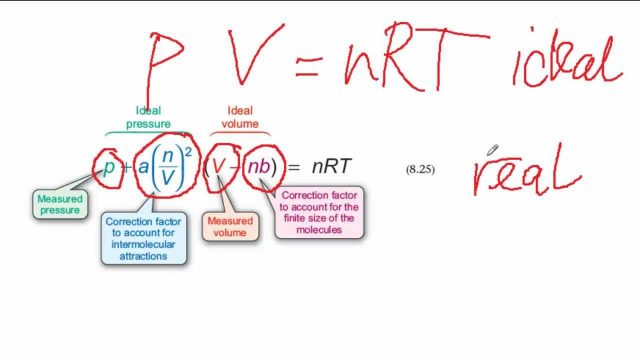
In 1873, the Dutch physicist Johannes D. van der Waals suggested a corrected version of the ideal gas law. It is one of the simpler equations of state for real gases and is referred to as the van der Waals equation. In it van der Walls introduced two constants, a and b, different for each gas. The van der Waals constant a represents the pressure correction and is related to the magnitude of the interactions between gas particles. The van der Waals constant b is the volume correction and is related to the size of the gas particles. The values of these constants are determined experimentally. Unlike a virial equation, which fits behaviour of real gases to a mathematical equation, the van der Waals equation is a mathematical model that attempts to predict behaviour of a gas in terms of real physical phenomena (that is, interaction between gas molecules and the physical sizes of atoms).

It was Fritz London in 1930 who gave a quantitative theory in terms of quantum mechanics of the interactions that J.D. van der Waals had described: forces that are attractive between atoms and molecules but are much weaker than valence bonds; they are inversely proportional to the seventh power of the distance between the atoms or molecules (recall that in the Coulomb interaction the inverse proportionality is to the square of the distance) . London found, for example, that if the molecules are some 10 nanometres or more apart then relativistic effects would change the variation of the force from the inverse of the seventh power to the inverse of the eighth power.

These attractive van der Waals forces are sometimes considered negligible and forgotten in the models of some physical systems. When considering how a diatomic gas like hydrogen or nitrogen may dissociate when adsorbed on the surface of a metal, a system very important to understand in catalysis, one may think that van der Waals forces are not important enough to be considered.

To study these systems, molecular beams are used. Actually, supersonic beams permit a fine control of the incidence angle and the translational energy of the molecules something very useful when characterising the dynamics of gas-surface interactions. But the experimental results using this technique show a discrepancy with theory when sticking coefficient is calculated for various incident conditions (angle and kinetic energy ) for a system such as nitrogen, N₂, on tungsten, W(110). It could be the case that the forgotten van der Waals forces may be a clue.

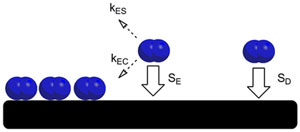
This is exactly what a team of researchers the Materials Physics Center UPV/EHU-CSIC and DIPC has shown¹ from first principles, that van der Waals should be considered, but still they alone are not enough to solve the mystery. The results are published in The Journal of Chemical Physics.

The team performed a systematic study on the dissociative adsorption using a selection of existing non-local functionals that include the van der Waals interaction; ab initio molecular dynamics was used. They found that the inclusion of the non-local correlation term contributed in all cases to correct the unrealistic energy barriers at large molecule-surface distances that were identified in the models that did not consider them.

Still they found that when comparing the obtained dissociation probabilities with existing experimental data, none of the used van der Waals functionals seems to provide altogether an adequate description of the N₂/W(110) interaction at short and large distances.

This analysis shows that a functional can accurately describe adsorption energies and energy barriers, but at the same time can fail in providing an overall description of the multi-configurational space that ultimately rules the complex gas-surface interaction.

Author: César Tomé López is a science writer and the editor of Mapping Ignorance.