Classical indeterminism, or Laplace’s Demon’s nightmare

Though I’m making a break in the brief story of skepticism I have been telling in my past entries, we will not lose contact with our friends the demons; if in that story we were talking about the most philosophical one of them (Descartes’ Evil Demon), this time our initial protagonist is another, not less famous, demon: the one invented by the French physician, astronomer and mathematician Pierre-Simon de Laplace (1749-1827). Laplace’s demon was introduced in his book Essai philosophique sur les probabilités (1814), and it incarnated in the clearest way our common idea about what physical determinism consists in:

“An intellect which at a certain moment would know all forces that set nature in motion, and all positions of all items of which nature is composed, if this intellect were also vast enough to submit these data to analysis, it would embrace in a single formula the movements of the greatest bodies of the universe and those of the tiniest atom; for such an intellect nothing would be uncertain and the future just like the past would be present before its eyes”.

As it became even clearer much later, Laplace’s formulation invited to separate two different concepts: predictability and mathematical uniqueness. Determinism would not consist just in the possibility of predicting the future from the past or from the present, but in the fact that this possibility is a property of the mathematical laws that describe nature. It is not that we can predict every future event; it is rather that this prediction would be possible for an intelligence capable of determining in a complete way the current state of movement of each and every material particle in the universe, and of computing the equations that would describe those movements. Thanks to the work of Poincaré one century after Laplace, and to the modern mathematical theory of chaos he helped to develop, we already know that a system can be perfectly deterministic in Laplace demon’s sense while however being highly or even totally impredictable in practice under most circumstances. It is what we call ‘deterministic chaos’ or ‘sensitivity to initial conditions’. Paired with the discovery that the notion of ‘the precise state of movement’ of a particle makes no physical sense in quantum mechanics, this inflicted a (definitive?) blow to the dream of having a perfectly predictive knowledge of our universe, if someone had had this dream sometime. The tryumph of quantum physics also helped to spread the message that contemporary physics, contrarily to that of Newton or Laplace, was indeterministic instead of deterministic. Laplace’s demon could not have all the past and the future ‘present before its eyes’ because the true laws of nature do not allow that mathematically: at some point, the best thing the demon could deduce from those laws would be just probabilities, not certainties.

This is all pretty familiar. But what is probably much less well known is that Laplace was simply wrong regarding, not the ‘true laws of nature’, but the laws he thought were the true ones, i.e., the laws of Newtonian mechanics… or well, let’s say at least that he was very likely wrong. You have read it well: the laws of classical mechanics are not deterministic in Laplace’s sense. Of course, this does not imply that all possible physical systems obeying Newtonian laws are indeterministic; only that some Newtonian systems are so. By one of the typical ironies of History, the reason why this is true had been discovered just a few years before Laplace told about his demon, and by another great French mathematician, Siméon Denis Poisson (1781-1840), who in 1806 had proved that some systems of differential equations applicable to moving objects admitted more that one solution. In particular, Poisson considered medium resistance laws of the form dv/dt = −avⁿ and d²x/dt² = axⁿ, and discovered that for 0 < n < 1, and 0 < |n| < 1, there are different non-trivial solutions when the initial velocity was zero. Of course, Poisson did not interpret his mathematical conclusion as a discovery about whether the universe is or is not deterministic in the physical sense; he just assumed that besides the equations he was considering, there would be some additional mathematical condition that nature imposes on the systems containing that ‘failure’, a condition that scientists should try to discover. Poisson’s equations were often discussed from a mathematical point of view, but hardly in connection with the problem of determinism, save by the also French scientist Joseph Boussinesq, who, in a book published in 1878 (Conciliation du véritable déterminisme mécanique avec l’existence de la vie et de la liberté morale), saw this type of scape from the powers of Laplace’s demon as the locus where free will could reside (a little bit like Lucretius’ idea of clinamen, a kind of random deviation on the otherwise straight natural movement of atoms, would also underlie our capacity of taking free decisions). But this was mostly ignored, and the advent of quantum mechanics a few decades later offered an apparently more provisory way for those willing to ‘reconcile’ human free will with natural science.

In the last decades, a number of other types of systems failing to satisfy the Laplacean notion of determinism have been proposed and studied. One the most famous is the one called ‘Alien Invasion’ (Bernadete, 1964): since classical mechanics does not put a limit to the velocities a body may have, it is possible under Newtonian laws that an object accelerates till having an infinite velocity (or more exactly, that it reaches any finite velocity before time t). Such an asymptotically accelerating body will just disappear from the universe at time t. But remember that classical mechanics is also time reversible: if a system obeys its laws, then a second system which is equal to the first one, but in which the temporal order has been inverted, will also fulfil the same laws. Hence, how would it look like a system that is just a temporal inversion of the one with our infinitely accelerated body? It will be a system in which an object just appears, coming from an infinite distance at time t. But nothing before time t could have helped us (nor Laplace demon) to calculate that the body will be appearing at a precise moment. So the appearance of the object would be a totally chance event.

Another example is known as the ‘Mercedes star’. Imagine three identical mass points moving on the same plane, approaching simultaneously the centre of a circle at exactly the same velocity, and in straight trajectories that are at 120º of each other. What will Newtonian mechanics predict that it will happen after the objects collide at the centre of the circle? The truth is that there is no determinate prediction; in principle, it depends on how one makes the calculations, but all trajectories such that the distance of 120º between the bodies is preserved are compatible with Newtonian laws.

A third example (Pérez Laraudogoita, 1996) is inspired by the Zeno’s paradox of Achilles and the Tortoise, and as the ‘Alien Invasion’ case, requires considering both infinites and time reversal. Imagine a line of unit distance in which we place a mass point at its right extreme, i.e., at distance 1 from the origin 0; an identical second mass point will be at distance ½, a third one at 1/3, and so on, and so forth. There will be an infinite number of such objects between 0 and 1, hence, densely concentrating as they are closer to 0. Suppose now that the first object starts moving towards the others, with a velocity equal to 1. The classical laws of collision mechanics predict that this object will collide with the second one in ½ units of time, and stop at the same place where the second object stayed, displacing the second object with the same velocity in the direction of the third one, and then stop there, etc., etc. But we will not observe that, after 1 unit of time (the time needed for all the collisions to take place between points 1 and 0), some object starts moving from 0 to the left, carrying with it the momentum that the first object had at the beginning of our thought experiment, for… which object will it be? For any of the infinite number of objects between 1 and 0, there is always some other object to its left, so it will not be the one that ‘escapes’ from point 0. Besides this paradoxical effect of ‘missing momentum’, what is interesting for the present discussion is what would it happen if we subject this system to a time reversal (something totally compatible with classical mechanics): in this case what we will have is that our mass points start moving towards the right spontaneously, for there were nothing initiating the movement. This is obviously another violation of determinism.

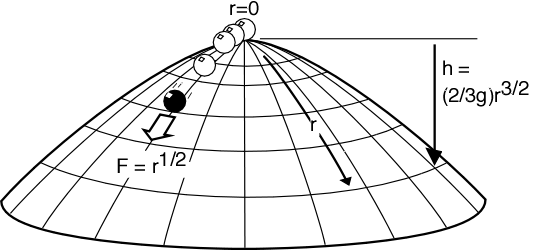
The last example I am going to mention is due to the philosopher John Norton, and is known as ‘Norton dome’ after him. Imagine a ball sitting at the apex of a frictionless ‘dome’, in particular, a solid constructed by the revolution of a curve described by the equation h = (2/3g)r^3/2, where h is the vertical distance from a point on the surface of the dome to its vertex, and r is the distance between both points measured on the surface of the dome. Norton proved that, besides the obvious solution in which the ball remains at rest at the apex indefinitely, there is another set of solutions, in which the ball starts falling spontaneously in any direction from the apex of the dome. This has nothing to do with quantum or thermodynamic microscopic ‘fluctuations’ of the material with which the ball or the dome are constructed, but just derives from the mathematics of the equation according to which the surface of the dome has been constructed.

In conclusion, it seems that it was not necessary to reach the mysteries of quantum physics to provoke a nightmare to the poor demon of Laplace.

REFERENCES

Earman, J., 1986, A Primer on Determinism, Dordrecht: Reidel.

Norton, J. D., 2008, “The Dome: An Unexpectedly Simple Failure of Determinism,” Philosophy of Science, 75: 786–98.

Pérez Laraudogoitia, J., 1996, ‘A Beautiful Supertask’, Mind, 105: 81–83.

Poisson, S. D., 1806, “Mémoire sur les solutions particulières des équations différentielles et des équations aux différences”. Journal de l’École Polytechnique, XIII e cahier, t. VI., 1806, pp. 60-125.