How do we know atomic stationary states are real?

Condensed matter • DIPC • History • Physics • Science

By DIPC June 16, 2016 0 comments Print

stationary states — Franck-Hertz experiment with neon gas: 3 glowing regions

The success of Bohr’s model of the atom in accounting for the spectrum of hydrogen left this question: Could experiments show directly that atoms do have only certain, separate energy states? In other words, are there really gaps between the energies that an atom can have? A famous experiment in 1914, by the German physicists James Franck and Gustav Hertz (a nephew of Heinrich Hertz), showed that these separate energy states do indeed exist.

Franck and Hertz bombarded atoms with electrons from an “electron gun,” a hot wire that emitted electrons which were then accelerated through a hole leading into an evacuated region where they were aimed at a target. Franck and Hertz were able to measure the energy lost by the electrons in collisions with the target atoms. They could also determine the energy gained by the atoms in these collisions.

In their first experiment, Franck and Hertz bombarded mercury vapor contained in a chamber at very low pressure. The procedure was equivalent to measuring the kinetic energy of electrons on leaving the electron gun, and again after they had passed through the mercury vapor. The only way electrons could lose energy was in collisions with the mercury atoms.

Franck and Hertz found that when the kinetic energy of the electrons leaving the gun was small (up to several electron volts), the electrons still had almost exactly the same energy after passage through the mercury vapor as they had on leaving the gun.

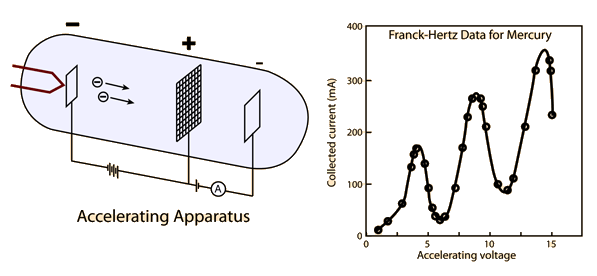
This result could be explained in the following way. A mercury atom is several hundred thousand times more massive than an electron. When it has low kinetic energy, the electron just bounces off a mercury atom, much as a golf ball thrown at a bowling ball would bounce off. A collision of this kind is called an “elastic” collision. In an elastic collision, the mercury atom (bowling ball) takes up only a negligible part of the kinetic energy of the electron (golf ball), so that the electron loses practically none of its kinetic energy.

But when the kinetic energy of the electrons was raised to 5 eV, the experimental results changed dramatically. When an electron collided with a mercury atom, the electron lost almost exactly 4.9 eV of energy. When the energy was increased to 6.0 eV, the electron still lost just 4.9 eV of energy in collision, being left with 1.1 eV of energy. These results indicated that a mercury atom cannot accept less than 4.9 eV of energy. Furthermore, when the mercury atom is offered somewhat more energy, for example, 5 eV or 6 eV, it still accepts only 4.9 eV.

The accepted amount of energy cannot go into kinetic energy of the mercury because the atom is so much more massive than the electron. Therefore, Franck and Hertz concluded that the 4.9 eV is added to the internal energy of the mercury atom; that is, the mercury atom enters a stationary state with an energy 4.9 eV greater than that of the lowest energy state, with no allowed energy level in between.

What happens to this extra 4.9 eV of internal energy? According to the Bohr model, this amount of energy should be emitted as electromagnetic radiation when the atom returns to its lowest state. Franck and Hertz looked for this radiation, and they found it! They observed that the mercury vapor, after having been bombarded with electrons, emitted light at a wavelength of 253.5 nm. This wavelength was known to exist in the emission spectrum of hot mercury vapor. The wavelength corresponds to a frequency f for which the photon’s energy, hf, is just 4.9 eV (as you can easily calculate). This result showed that mercury atoms had indeed gained (and then radiated away) 4.9 eV of energy in collisions with electrons.

Later experiments showed that mercury atoms bombarded by electrons could also gain other sharply defined amounts of energy, for example, 6.7 eV and 10.4 eV. In each case, the subsequently emitted radiation corresponded to known lines in the emission spectrum of mercury. In each case, similar results were obtained: the electrons always lost energy, and the atoms always gained energy, both only in sharply defined amounts. Each type of atom studied was found to have separate energy states. The amounts of energy gained by the atoms in collisions with electrons always corresponded to the energy of photons in known spectrum lines. Thus, this direct experiment confirmed the existence of separate stationary states of atoms as predicted by Bohr’s theory of atomic spectra. This result provided strong evidence of the validity of the Bohr model.

Frank and Hertz received for this work the Nobel Prize in Physics 1925.