A link between straintronics and valleytronics in graphene
So-called “valleytronics” is a new type of electronics that could lead to faster and more efficient computer logic systems and data storage chips in next-generation devices. Valley electrons are so named because they carry a valley “degree of freedom.” This is a new way to harness electrons for information processing that’s in addition to utilizing an electron’s other degrees of freedom, which are quantum spin in spintronic devices and charge in conventional electronics.
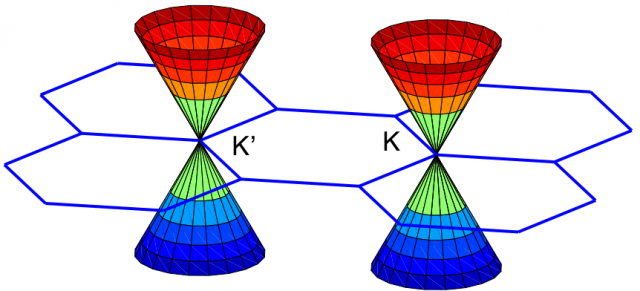
On the atomic scale, matter behaves as both a particle and a wave. Electrons, therefore, have an associated wavelength that usually can have many different values. In crystalline systems however, certain wavelengths may be favored. Graphene, for example, has two favoured wavelengths known as K and K’ (K prime). This means that two electrons in graphene can have the same energy but different wavelengths – or, to put it another way, different “valley.”
Electronics use charge to represent information, but when charge flows through a material, some energy is dissipated as heat, a problem for all electronic devices in use today. However, if the same quantity of electrons in a channel flow in opposite directions, no net charge is transferred and no heat is dissipated – but in a normal electronic device this would mean that no information was passed either. A valleytronics device transmitting information using pure valley current, where electrons with the same valley flow in one direction, would not have this limitation, and offers a route to realizing extremely low power devices.
Thus valleytronics is currently under intensive research, not only concerning graphene but also other two dimensional (2D) materials. Indeed, the generation of valley currents has been recently demonstrated in graphene devices deposited on a hexagonal boron nitride (hBN) substrate. The effect of the hBN substrate is to break the symmetry between the two sublattices of the honeycomb lattice, which opens an energy gap at the (Dirac) point where the conduction and valence bands meet. This leads to a valley-polarized current in the bulk transverse to the applied electric field . This phenomenon, known as the valley Hall effect (VHE), can be detected as large enhancement of the nonlocal resistance in a Hall bar device.
Now, in a work 1 coordinated by DIPC’s Miguel A. Cazalilla, researchers present a different approach to generate valley-polarized currents in graphene, which relies on nonuniform strain. These predicted currents are neutral currents that do not couple to external magnetic fields. The hallmark of this strain-induced VHE being the emergence of a large nonlocal resistance in Hall bar devices.
Since strain can be controlled more easily than the magnitude of the hBN-induced gap, it will allow for a larger tunability of the effect, thus providing a novel link between valleytronics and straintronics. In graphene and other 2D materials strain can be described as a (pseudo) gauge field, which induces a (Aharonov–Bohm-like) phase in real space.
The researchers develop a theory of the strain-induced VHE using the quantum Boltzmann equation, and deriving the microscopic equations governing the diffusion of valley polarization. Then, they solve these equations for a Hall bar device geometry subject to nonuniform strain leading to uniform pseudo-magnetic field.
The strain-induced VHE that the researchers predict should be observable with fairly modest strain levels in Hall bar devices. By ‘modest strain’, they mean strain levels that could be achieved simply by stretching one edge while clamping the other in a Hall (H-shaped) device. Interestingly, the results apply to devices in the micrometer scale, where conduction takes places in the diffusive regime. Devices thar are potentially much more interesting from the application point of view than nanometer-sized ones.
Author: César Tomé López is a science writer and the editor of Mapping Ignorance.
References
- Xian-Peng Zhang, Chunli Huang, and Miguel A Cazalilla (2017) Valley Hall effect and nonlocal transport in strained graphene 2D Mater. 4 – 024007 doi: 10.1088/2053-1583/aa5e9b ↩