Electronic friction is fundamental to understand surface chemistry dynamics

Anyone who has studied, even superficially, some thermodynamics has encountered the word adiabatic very early. This is because adiabatic processes are extremely useful to understand the basics of the field. An adiabatic process is any process that occurs without heat (or matter) entering or leaving a system. In general, an adiabatic change involves a fall or rise in temperature of the system.

But words may be misleading if we switch from the classical, macroscopic, phenomenological realm of thermodynamics to that of quantum mechanics, where adiabatic means something related but completely different. In quantum mechanics, an adiabatic approximation is one where the time dependence of parameters, such as the inter-nuclear distance between atoms in a molecule is slowly varying. This slow-motion behaviour means that the solution to the Schrödinger equation that defines de system at one point in time goes continuously over to the solution at a later time. This kind of approximation was developed by Max Born and Vladimir Fock.

A very common adiabatic approximation used in molecular and condensed matter physics is the Born-Oppenheimer one. In it the motion of atomic nuclei is taken to be so much slower than the motion of the electrons that, when calculating the motions of electrons, the nuclei can be taken to be in fixed positions. This approximation is very successful, but it is known to be not completely true.

For example, what would happen if we had a gas interacting with a metal surface and a chemical reaction is taken place? We would have ions moving in metal electronic gases for a while. In this conditions, as Pedro Echenique and others demonstrated¹, we could expect a friction effect, an electronic friction, a stopping power of an electron gas for slow ions. But this electronic friction is also a source of electronic nonadiabaticity or, from another point of view, a way of losing energy needed for the main chemical reaction.

The study of these ways of losing energy in surface reactions, especially catalytic ones, is terribly important in technological applications. But, quite paradoxically, to date, most accurate solutions of the full nuclear-electron wave function are restricted to systems of the complexity level of gas-phase H₂⁺. For other systems approximations are far less rigorous, using a combination of quantum and classical dynamics. Still, the imposed computational burden nevertheless still restricts their practical use to simple metals and subpicosecond time scales, to symmetric adsorbate trajectories, or to only qualitative accounts of the metal electronic structure.

An efficient way, in computational-demand terms, of producing calculations with predictive power and material specific trajectories would be to correct the Born-Oppenheimer approximations with classical molecular dynamics that could incorporate the concept of electronic friction. Some recent attempts has been done using still another approximation, that atoms are independent, so that the computational cost is further reduced. But is this approach successful?

Now a group of researchers, that includes Iñaki Juaristi from Materials Physics Center – UPV/EHU and DIPC, perform a substantiated assessment of the quality of the nonadiabatic description. They find ²that the approximation is qualitatively good but not perfect. They propose a way to further improve it.

In the study, accurate experimental reference data are used, primarily focusing on the internal stretch mode of two systems which have been studied most extensively and conclusively by experiments: CO adsorbed on Cu(100) and Pt(111).

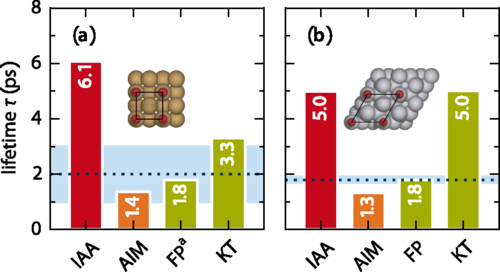
The authors find that rather than an explicit account of the surface band structure, the analysis suggests that missing intramolecular contributions are the reason for the main differences, as one would expect from the atom independency assumption and the neglect of intramolecular effects. But also that approximately incorporating such contributions through an atoms-in-molecules (AIM) numerical calculation indeed yields consistent lifetimes for a range of diatomic adsorbate systems.

The presented AIM alternative accounts for energy dissipation approximately through a charge partitioning scheme. As it effectively treats the molecular electrons as part of the metallic substrate, it is expected that the AIM friction concept to generally rather overestimate nonadiabatic energy losses and to perform best for chemisorbed adsorbates at close distances to the surface.

The results consolidate the importance of approximations that incorporate electronic friction in the study of the technologically critical catalytic systems.

Author: César Tomé López is a science writer and the editor of Mapping Ignorance.