Breakdown of the free electron gas concept for electronic stopping

There is a variable that is relevant for such seemingly different fields as outer space exploration , nanotechnology , fusion research , or medicine. And that is electronic stopping, its precise knowledge important for the understanding of space weathering, ion beam patterning, plasma-wall interactions, or radiation therapy, respectively.

When ions propagate in matter, they are decelerated due to the interaction with both nuclei and electrons—in other words, by nuclear and electronic stopping, respectively. The mean energy loss per path length is given by the deceleration force, i.e., the stopping power S = dE/dx. To

describe the interaction with atoms or molecules, often the stopping cross section (SCS) ε = 1/n · dE=dx is used, where n represents the atomic or molecular density of the target material, respectively. This SCS has dimensions of energy, and can be described as the energy loss per atom per unit area perpendicular to the particle (ion) motion. Being SCS a quite fundamental quantity, it is mandatory to have a detailed understanding of the prevailing energy loss mechanisms.

At high ion velocities, energy loss of ions is dominated by electronic stopping. In this regime, light ions represent only a weak perturbation for the target electrons. For low ion velocities, both electronic and nuclear collisions contribute to the stopping power. In this regime, the electronic energy loss is predominantly due to the interaction with valence electrons.

SCS has been studied using a free-electron gas model with some success, but limitations of this model have been discovered for noble metals at very low proton velocities. But why does the model fail?

An international team of researchers, including some from UPV/EHU, DIPC and CFM, present ¹ evidence that the free-electron gas model fails when applied to metals with d or f bands of high density of states, like in transition and rare earth metals. The density of states being the number of states per interval of energy at each energy level available to be occupied.

They come to that conclusion after studying low-velocity hydrogen and deuterium ions stopped by foils of pure polycrystalline tantalum (Ta) and gadolinium (Gd), and comparing the results with those for platinum (Pt) and gold (Au).

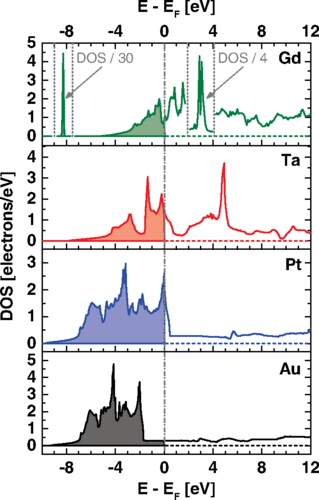
The researchers found that the electronic stopping of slow protons in tantalum and gadolinium is so efficient that any free-electron gas model fails to describe the slowing down process, leading to absurdities, like gadolinium (64 electrons) and aluminium (13 electrons) having the same density parameter.

They conclude that elaborate many-body theoretical models are required to thoroughly understand the underlying physical mechanisms and to find possibly a way of predicting realistic stopping power values for rare earth and transition metals even for simple ions.

Author: César Tomé López is a science writer and the editor of Mapping Ignorance.