Numerical cognition: numbers and brain plasticity

Numerical cognition is a subdiscipline of the cognitive sciences that studies the neural, developmental and behavioral bases of the use of numbers and mathematics. It is a multidisciplinary field in which cognitive psychology, developmental psychology, cognitive linguistics and neuroscience participate.

Numerical cognition is fundamental for everyday activities, starts early in development and significantly improves with the appearance of symbolization through the acquisition of language and learning in the classroom. In schooling, children learn a wide range of mathematical tools and one of the first and most important is to associate a quantity (analogue system) with its symbol, a word or a written number (symbolic system). Transcoding between analog and symbolic systems is the fundamental substrate of much later mathematical knowledge and the basis for incorporating more sophisticated numerical tools into the student’s skills.

One curious aspect is that animals also have that approximate sense of quantity, which is called numeracy. If a rat, for example, is trained to press a lever 8 or 16 times, thus obtaining a reward of food, it is seen that the number of times that it pulses follows a normal distribution with a peak around 8 or 16, the preset amount. If the rats are hungry, they press the lever faster, but the number of pressures is the same. Numbers also serve to assess situations. One research group ¹ emitted a number of roars through a loudspeaker in the African savannah, near a group of lions. If they did three roars and a lioness was alone, she walked away. Instead, if she was with four sisters and heard the same three roars, they would approach and explore, indicating that they had an estimative criterion of when they were “outnumbered”.

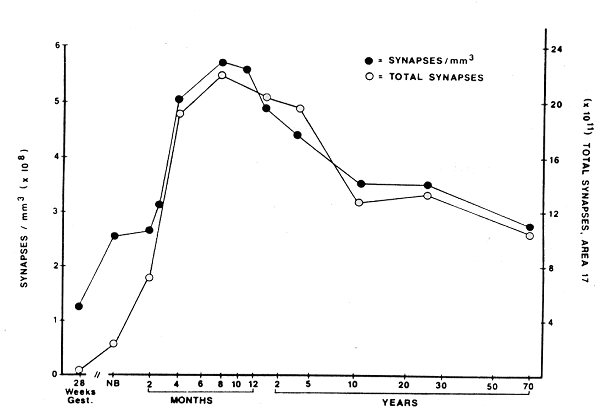
Does numerical learning and the transcoding system produce brain changes? It is an important question because other educational issues like reading and writing do. The answer is yes, but it is a complex process of measuring for the next reason. The cerebral maturation advances in two overlapping levels: on the one hand a genetic program that follows step by step in an orderly and successive way; on the other a series of environmental influences that modulate that program and generate changes, sometimes subtle, in other enormously striking. The genetic program generates a proliferation of neurons and synapses that later are eliminated progressively, in a fast pruning, leaving only those that have established functional connections. It is therefore a non-linear process, with a sudden increase in the number of neurons and another not-so-sudden decrease, which continues to show changes at more advanced ages. Thus, the gray matter shows a loss of density over time, which is related to a synaptic pruning during adolescence and early youth. On the other hand, the synaptic plasticity of the brain is evident in early childhood itself and the result of learning programs, such as those occurring in the family and in the classroom, is that an increase in gray matter. It would be like when we go to gymnasium and our muscles increase in size, here we are exercising the areas involved in the cerebral processing of mathematics. It is a specific process and, for example, numerical training produces more important changes in the regions involved in those tasks and in groups specialized in using such functions as, for example, mathematicians.

The most important regions appear to be the intraparietal sulcus (IPS) and the lower parietal lobe (IPL), two intensely active areas when someone is asked to do mental calculations. The functions seem to be different and the IPS hosts the circuits involved in numerical estimation, numerical comparison and mental calculation, something that is usually studied with subtractions. The IPL intervenes in tasks that require a formal and intense learning such as multiplication. In fact, as a result of a stroke there are patients who may lose the ability to subtract but not to multiply, and vice versa.

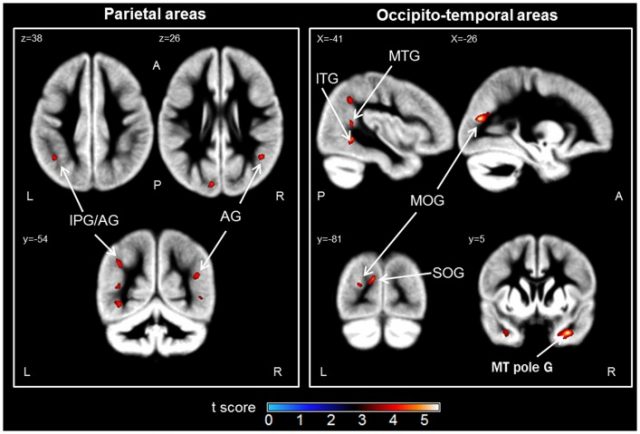
The next question, and is not banal, is the children who have better numerical learning, have brain changes more marked than those of their colleagues in which that mathematical domain is less? The answer is also yes. Lubin and his group ² have used a technique called voxel-based morphometry that allows the measurement and study of anatomical differences between different brains. They applied this technique to 22 children of ten years of age who differed in their ability to transcode between the analog and digital systems.

The main results were that children with a lower numerical ability had a lower volume of gray matter in the parietal cortex (particularly in the left IPS and in the bilateral angular gyrus) and in the occipito-temporal area. From all these regions it is known that they participate in the process of transcoding between analog and symbolic systems.

And what about children with dyscalculia, the difficulty in learning the principles of calculus caused by a brain problem that hinders the use of the symbolic system? The MRI study of dyscalculic children and controls shows that the first ones present a smaller gray matter, especially in cortical parietal and frontal regions, such as the left IPS and the middle and inferior frontal gyri. Children with dyscalculia who have a “number sense” deficit (e.g., difficulties in understanding a quantity) have a loss of gray matter in the bilateral parietal areas compared to control children. As in the rest of the studies, it is difficult to know whether the smallest gray substance in the “numerical areas” prevents them from a good mathematical operation or, if it is the reverse, and the little taste for mathematics generates in a certain way an atrophy of the regions involved in the management of numbers.

Joining neuroscience research with education is a fundamental process for understanding how children learn. Neuroimaging techniques allow us to see the cerebral changes associated with learning and seem a way to achieve a better quality of education and a pedagogy more adapted to the reality, including biological reality, of our children. We can have measurable references, for example, to see if a therapeutic strategy or a concrete pedagogical approach is improving the density and extension of the brain areas involved, providing evidence to add to the results of tests and exams. On the other hand, we are still not being able to produce direct applications for the classroom, an increasingly clear demand and that is being covered sometimes by proposals without scientific basis.