Einstein’s brain and numerical cognition: a chicken-and-egg story?

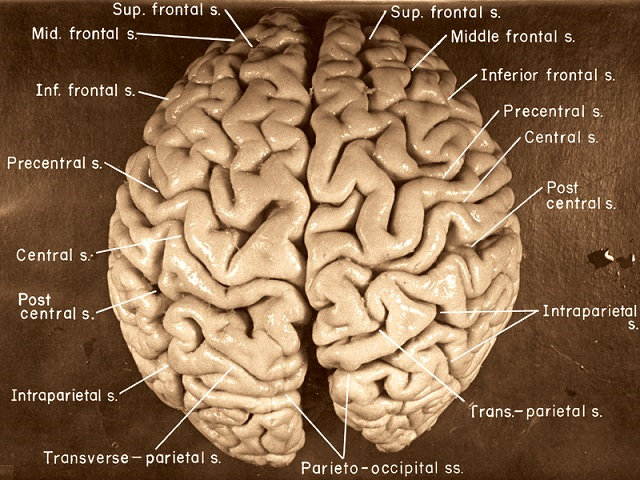
The Mütter Museum in Philadelphia is one of those must go places for any brain enthusiast. The collection beautifully represents the history of modern medicine, including a repository of skulls used in phrenological studies, broken cranial bones à la Phineas Gage, diseased coronal cuts, American civil war surgical memorabilia, and a great little gem: a cut up of the brain of one of the brightest minds of the 20^th century – Albert Einstein.

More than 60 years ago, Princeton’s pathologist Thomas S. Harvey conducted Einstein’s autopsy within 7 hours of his death and decided to “pickle” our star’s brain in formalin. The specimen remained under Harvey’s possession until 1978, when a journalist rediscovered it¹. About 5 years ago, the museum bought forty-six (of a total of approximately 240) microscope-ready brain slices and prepared a small display in a structure that looks a bit like an old phone booth – this is somewhat modest considering the caliber of the physicist.

Looking at Einstein’s brain at the Mütter is mesmerizing. They even have a slice of his temporal lobe showing the hippocampus! If possible, how amazing would it be to extract some of his teaching memories in Berlin and Zurich, the move to New Jersey, or even some of his numerical thoughts at age 26 – the so called miraculous year when the mass-energy equivalence formula came to light ²?

What most strikes the mind of the Mütter’s visitor is a little narrative about the differences of Einstein’s brain with what we all have – let’s call it an average brain supporting an average cognition. Long gone are the times in which ancient scholars thought that the brain functioned as a cooling system, a radiator to refresh the desires of the heart. Today, the brain stands as a hinge for our understanding of the mind, and the more we learn about it, the more we are able to understand differences among healthy individuals, the disruption of behavior in disease and how to treat motor and cognitive disorders after stroke, dementia, or other neurological diseases.

But, how much of Einstein’s physics, math fad, and numerical superpowers can be explained just by looking at his brain?

There are many hypotheses out there regarding the virtues of our physicist’s brain. An interesting one is a malformation of the anterior part of the Sylvian fissure – one of the two biggest grooves in each of our brain hemispheres separating the frontal lobe from the temporal lobe. Prof. Sandra F. Witelson and colleagues ³ discussed this issue by bring us back to a time early in the 20^th century when the brains of outstanding people such as Bach or Descartes were scrutinized in a quest for the basis of intelligence. One of the caveats of those studies is that the brains were not consistently preserved or even compared with a control group.

The study by Witelson et al. is unique as it contains rather large samples of brain specimens without psychiatric disorders and normal cognitive abilities. This allowed the authors to objectively report no differences between Einstein’s brain and controls in weight, length, height, and size of the corpus callosum – a white matter bundle connecting the two hemispheres. More importantly, the authors described Einstein’s unusual brain anatomy by indicating that “the posterior ascending branch of the Sylvian fissure [was] confluent with the postcentral sulcus” and that, consequently, his brain did not have the anterior part of the supramarginal gyrus (a common structure in the parietal lobe). Moreover, the parietal lobes in both of Einstein’s hemispheres were 15% wider (about 1cm) and more spherical than those of controls!

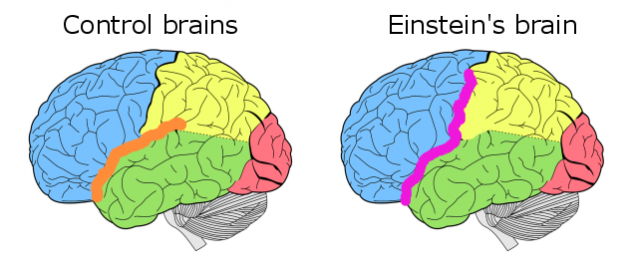
So what is so special about the parietal lobes and what can this tell us about Einstein’s outstanding numerical abilities?

There are multiple cognitive neuroscience methods that can help us to study this question, from natural lesion studies in people with neurological disorders, measuring brain waves with electroencephalography or temporarily knocking down brain areas with transcranial magnetic stimulation, to very expensive, yet tremendously rewarding techniques such as functional magnetic resonance imaging or magnetoencelphalography. Here, we will describe evidence from two surgical studies on numerical cognition. The beauty of surgical studies is that they represent, literally speaking, an open window to the brain. That is, an opportunity to look inside our thinking radiator in vivo, while making it possible to draw causal inferences about the brain and cognition.

John Whalen and colleagues ⁴ reported the case of a young individual with epilepsy to whom they performed a craniotomy and implanted various grids of electrodes. The primary idea of these grids is to measure electrical activity over directly in the cortex, hence, obtaining a much better spatial resolution to locate the epileptic focus before the surgery. Moreover, patients can be asked to undergo certain tasks to locate specific cognitive functions in the brain or, as it is the case of this study, to gain a better understanding of how and where numerical aspects of cognition happen in the brain.

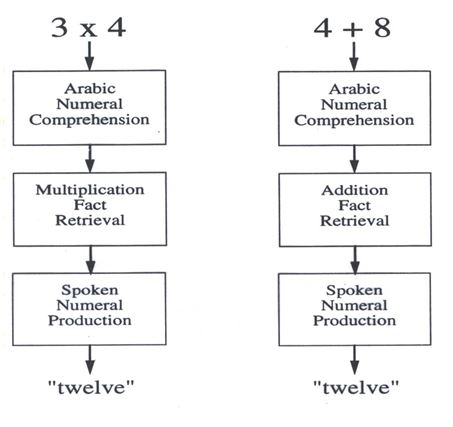
Whalen et al. studied the involvement of the left parietal lobe in multiplication by inducing a “short temporal lesion” in the brain. This was possible by applying a low intensity electrical current in two electrodes of the grid at a time, while asking the patient to perform a simple multiplication task (e.g., 5 x 1 = 5; 7 x 7 = 49). In accordance with previous findings from studies in people with permanent lesions, the authors found that electrical stimulation of the parietal lobe – close to the different area in Einstein’s brain – disrupted the capacity of our patient to multiply. By itself this is an interesting finding, as stimulation in other brain areas did not disrupt the patient’s multiplication performance. Now, one of course could think that electrical stimulation induced errors in cognitive functions necessary to perform the task. For example, understanding the shapes of Arabic numbers, or saying the numbers out loud.

While this may be true, a qualitative analysis of errors and a second experiment where the authors included both a multiplication and an addition task (hence, a second task that also required the patient to understand the shapes of Arabic numbers and say the numbers out loud) demonstrated that the left parietal lobe is heavily involved in multiplication. This is because during stimulation the patient could not multiply but add the numbers in the multiplication (e.g., *5 x 1 = 6; 7 x 7 = 14) and, also, when he produced a significantly smaller number of errors in addition than in multiplication.

In a similar and more recent study, Alessandro Della Puppa, Carlo Semenza and colleagues ⁵ studied the role of the right parietal lobe in numerical cognition. The authors assessed three individuals with a brain tumor in the right parietal lobe. In this population, electrical stimulation is typically used during surgery, right after the craniotomy, to locate brain areas responsible for different cognitive functions. Similar to the work of Whalen et al., these researchers used a simple multiplication and addition task, and found that the inferior part of the right parietal lobe was implicated in calculation. More specifically, in two patients stimulation to this site induced calculation errors only in multiplication and in a third patient stimulation disturbed both multiplication and addition.

In sum, we all know that Albert Einstein was a superstar at numerical cognition. However, it is possibly more surprising to learn that his extraordinary abilities may have a brain basis, as it is precisely in places where his brain was different that cognitive neuroscientists have been able to discuss the role of multiplication and other mathematical abilities. Now, a chicken-or-egg question may arise: can we really reduce all of his numerical abilities to brain differences in relation to average control brains, or we should also acknowledge having had access to regular education, enrolling and finishing a doctorate degree, and long hours crunching numbers as the cause of his brilliance? In other words, did the brain differences cause his brilliance, or did his life experience cause his brain to change, resulting on the structural differences observed? Maybe a bit of both.