Beyond the point-dipole approximation

The wave nature of light expresses itself in the propagation all over space, showing an intrinsic limitation to be localized beyond the so-called diffraction limit which is of the order of half the wavelength of the photons propagating. However when interacting with matter, light often gets reflected, diffracted, scattered or absorbed depending on the interactions and excitations induced in the material. In particular, at visible wavelengths, between 450 nm and 800 nm, metals interact with electromagnetic waves producing a variety of optical effects. The conduction electrons that constitute the metal can oscillate rigidly at certain optical frequencies that depend on the electron density. Furthermore, when metals are physically bounded by surfaces and interfaces as it is usually the case in nanoparticles and nanostructures, the oscillations of the electron charge density at the surfaces show resonant localized modes so-called surface plasmons.

The interaction between surface plasmons and an ensemble of quantum emitters (quantum dots and organic molecules) can be pushed into the so-called collective strong coupling regime. This phenomenon takes place when light and matter states exchange energy faster than their respective decay channels, giving rise to new quasiparticles usually termed plasmon–exciton–polaritons. The properties of these hybrid states can be adjusted through their light and matter content, which means a new, and qualitatively different, degree of light manipulation.

It is apparent, then, that the strength of the coupling between molecular electronic excitations and cavity optical modes is a magnitude of paramount importance that determines the dynamical properties of important phenomena. The coupling strength between an emitter and an optical cavity (Figure 1) is often estimated as a product of the local electromagnetic field in the optical cavity, and the dipole moment of the emitter’s optically allowed electronic transition.

In this context, the molecular emitter is often considered to be a point-like dipole, since the dimensions of a typical optical cavity and thus the extension of its optical modes are usually orders of magnitude larger than the size of the emitter. However, nanoscale plasmonic resonators result in a class of optical cavities that allow for light localization into deeply subwavelength dimensions, thus reaching effective mode volumes as small as a few nanometers. Under these conditions, emitters such as quantum dots and organic molecules cannot be described as point-like objects any more, since the spatial extent of their electronic transition densities are of the order of the size of the strongly inhomogeneous local fields of the plasmonic resonator.

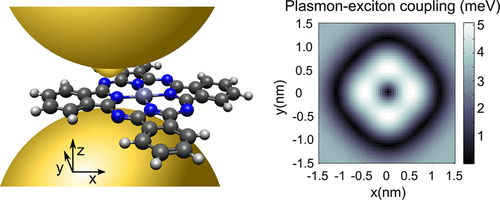
Now a team of researchers from CFM, UPV/EHU, DIPC and IFIMAC present ¹ a quantum theoretical framework that allows us to calculate the coupling between strongly confined plasmonic modes and molecular electronic excitations of spatially extended molecules, identifying the importance of a proper quantum treatment of the molecule to accurately obtain the dynamical properties of the hybrid exciton−plasmon system.

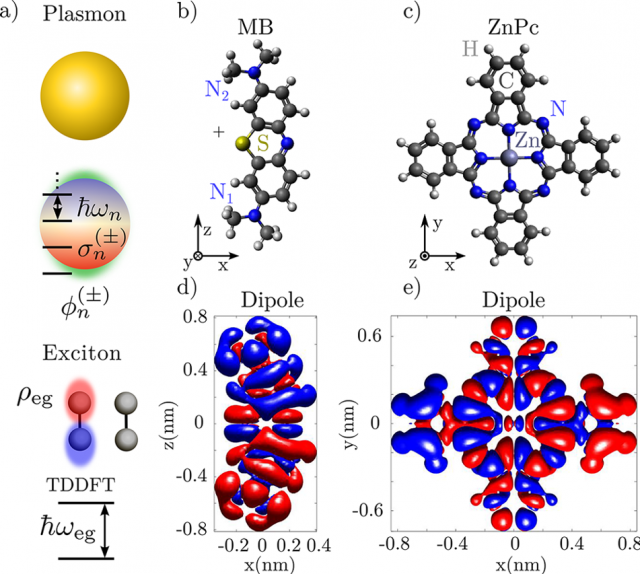
The resarchers use two exemplary organic molecules, methylene blue and zinc phtalocyanine (Figure 3), to reveal the importance of molecular size both in the weak and strong coupling regimes, as well as in the atomic-scale spatial mapping of the coupling strength.

The quantum treatment of the plasmon−exciton coupling combines the canonical quantization of plasmons in metallic particles with quantum chemistry calculations of molecular excitations based on the time-dependent density functional theory (Figure 3).

They show conclusively that the coupling strength stems from a delicate balance between the spatial dependence of both the excitonic transition charge density and the photonic fields, and therefore, only a quantum model that fully incorporates the inhomogeneities of the exciton transition charge density can describe quantitatively this interplay. Thus, each situation requires a detailed analysis as in some occasions the point-dipole approximation overestimates the coupling, whereas it underestimates its strength in others.

These results are of importance in nanoscale optical spectroscopy, in setting optical paths to engineer chemical reactivity at the single-molecule level, as well as in coherent control of the nanoscale light-matter interaction.

Author: César Tomé López is a science writer and the editor of Mapping Ignorance.