HOTI bismuth

The properties of bismuth have long defied classification, placing it in a category of its own. Now, as if it was not enough, it turns out its electronic structure has higher-order topology. This has been shown by an international team with the participation of Maia G. Vergniory (DIPC, Ikerbasque, UPV/EHU) and coordinated by Titus Neupert (University of Zurich)¹.

When we discussed the band theory of solids, we learned that electronic insulators are characterized by an energy gap between valence and conduction bands. Two insulators are classified as topologically equivalent, if one can be deformed to the other without closing this gap, while certain symmetries are respected. If time-reversal symmetry (TRS) is respected in this deformation process, three-dimensional insulators have been shown to fall into two disconnected topological classes: trivial and nontrivial. The latter are called topological insulators. (see Topological Quantum Chemistry, the band theory of solids is now complete).

What makes this mathematical classification highly relevant experimentally is the so-called bulk–boundary correspondence of topological insulators: the two-dimensional surface of a three-dimensional topological insulator hosts conducting states, with the dispersion of a non-degenerate Dirac cone, that cannot be gapped or localized without breaking TRS (or inducing interacting instabilities such as superconductivity or topological order). When, in addition, the spatial symmetries of the crystal are preserved during this deformation process, such as mirrors or rotations, one may speak of topological crystalline insulators. The additional symmetries have been argued to stabilize multiple Dirac cones on surfaces that are invariant under both TRS and the protecting spatial symmetry.

More recently, topological crystalline insulators were generalized to also include higher-order topological insulators (HOTIs, we discussed them here), in which gapless topological states protected by spatial symmetries appear at corners or hinges, while the edges and surfaces are gapped in two-dimensional and three-dimensional systems, respectively. HOTIs thus generalize the topological bulk–boundary correspondence.

Various topological aspects of the electronic structure of bismuth have been studied experimentally in the past. This revealed intriguing features such as one-dimensional topological modes localized along step edges on the surface of bismuth, conducting hinge channels on bismuth nanowires, quasi-one-dimensional metallic states on the bismuth (114) surface, and a quantum spin Hall effect in two-dimensional bismuth bilayers and bismuthene on silicon carbide.

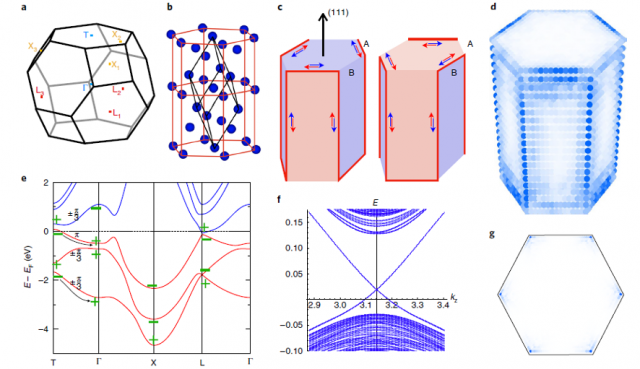
The bismuth–antimony alloy, Bi_1−xSb_x, was the first material realization of a three-dimensional topological insulator. The composition x was used to interpolate between bismuth, without band inversion, and the band-inverted antimony. In this work, the researchers demonstrate theoretically that the allegedly trivial end of this interpolation, bismuth, has in fact a three-dimensional topological band structure as well. Using band representations and the theory of topological quantum chemistry, the researchers show that bismuth is in fact a HOTI.

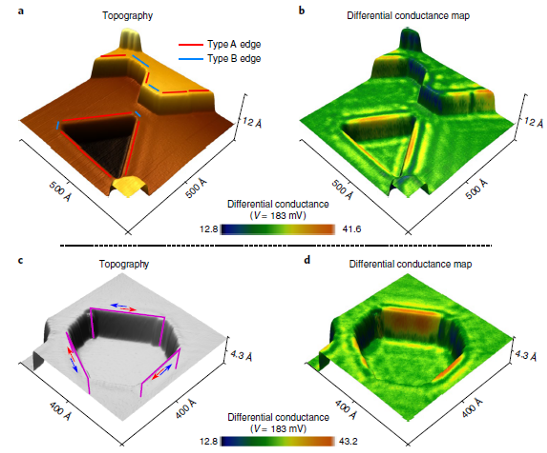
This finding provides a unified theoretical origin for all these previous experimental observations. The crystal symmetries that protect the topology of bismuth, Ĉ₃ rotation and inversion, establish a new class of HOTIs not discussed in previous works. This theoretical analysis is supported with experimental data using two complementary techniques: scanning tunnelling microscopy/spectroscopy (STM/STS) on surface step edges and Josephson-interferometry on bismuth nanowires. This result, thus, provides the first evidence of a three-dimensional HOTI in the electronic structure of a crystal.

The type of hinge states found may be used for lossless electronic transport owing to their local protection from backscattering by TRS disorder. Further applications include spintronics, owing to their spin–momentum locking, and—when proximitized with superconductivity—topological quantum computation. For the latter, a nanowire with hexagonal cross-section may provide a particularly convenient way of building a hexon: a group of six Majorana states, one at each hinge. Hexons have been proposed as building blocks for a measurement-only quantum computer.

Author: César Tomé López is a science writer and the editor of Mapping Ignorance.