First direct visualization by photoemision of how the Luttinger theorem works for Kondo lattices
Elements with 4f or 5f electrons in unfilled electron bands and their componuds , which have ions carrying magnetic moments but do not magnetically order, or only do so at very low temperatures, are generally known as heavy-fermion or heavy electron systems because the scattering of the conduction electrons with the magnetic ions results in a strongly enhanced (renormalized) effective mass, as in Kondo systems.
These Kondo lattices, where periodically arranged f local moments interact with the conduction electrons, represent here the outstanding class of materials in which the apparent “duality” of the f electrons, i.e. their simultaneous localized and itinerant behavior, gives rise to many novel quantum states of matter only recently discovered.
The central question for understanding the physics of heavy-fermion systems is how the Fermi volume is changed upon the localized-to-itinerant transition of the f moments. A fundamental guiding theoretical principle was established by the seminal realization of R. M. Martin that the Luttinger Fermi surface sum rule can be applied even to such strongly correlated systems as in the presently widely discussed YbRh2Si2.
The sum rule states that the Fermi-surface (FS) volume is conserved in the presence of interactions so long as the interactions do not produce a phase transition. In this context, the essence of the sum rule is that if the local orbital magnetic moments are quenched, for example by the Kondo effect, then the underlying local orbital electrons must be counted in the FS. If the moments are not quenched, for example in a magnetically ordered state, the underlying electrons are excluded from the FS. For the Kondo lattice, the sum rule is satisfied by the formation of heavy quasi-particle states at the Fermi energy, the analog of the Kondo resonance for a local orbital impurity site. These two situations are now known as the large and small Fermi surfaces, respectively.
In that regard, application of this Luttinger FS sum rule, known also as the Luttinger theorem, to the canonical heavy-fermion trivalent material YbRh2Si2 implies that its large f-derived Fermi surface in the paramagnetic Kondo regime should be similar in shape and volume to that of the divalent local moment system EuRh2Si2 in its paramagnetic regime.
The reasoning is that the Fermi surfaces of these two isoelectronic and isostructural materials in their paramagnetic states should enclose, for trivalent YbRh2Si2, one strongly correlated hole and N weakly correlated conduction band holes, and for divalent EuRh2Si2, N+1 weakly correlated holes. Thus, even if the Fermi surface masses are much different, the number of holes is the same for both systems, implying the large Fermi surface for both.
This audacious and simple proposition creates the tempting opportunity to explore an elegant realization of the Luttinger sum rule for the Yb-based Kondo lattice, in a way which has never been done before. Moreover, another exciting opportunity is to study EuRh2Si2 in its antiferromagnet (AFM) phase as a way to gain insight into how the anticipated large FS could be modified upon AFM order in the heavy-fermion Yb system. This knowledge is highly relevant for the mysterious AFM phase of YbRh2Si2below 70 mK which is a precursor of the quantum critical regime and superconductivity below 2mK established for this system.
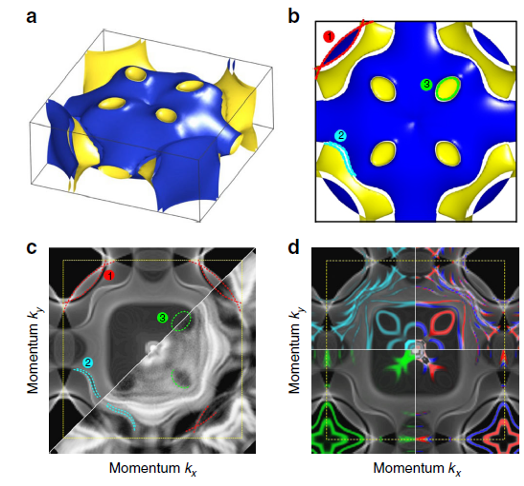
To comprehensively explore the aforementioned issues, we have applied 1 angle-resolved photoemission spectroscopy (ARPES) in UV and Soft X-ray modes to EuRh2Si2 and combined our experiment with ab-initio DFT calculations to EuRh2Si2. Our remarkable result is that, both in ARPES and DFT, the Fermi surfaces of both YbRh2Si2 and EuRh2Si2 materials are rather similar in size and shape, even though the masses of the dispersing electrons are heavy in the former, whereas they are light in the latter.
In summary, the primary novel findings of our work are:
i) We make an elegant demonstration of the Luttinger theorem for an Yb-based Kondo lattice and demonstrate how the large Fermi surface including the strongly correlated hole should look like. In fact, this is the first direct visualization by photoemision of how the Luttinger theorem works for Kondo lattices since its first proposition in 1982!
ii) We use EuRh2Si2 as an experimental and theoretical model system to infer important qualitative aspects of how the large Fermi surface in YbRh2Si2 might change upon AFM order below 70 mK – a mysterious phase, which is a precursor of quantum criticality and superconductivity in this system.
iii) Our ARPES measurements have also disclosed the curious property that the itinerant bulk-band states in the AFM phase characterized by ferromagnetic (FM) layers stacked antiferromagnetically become spin-polarized at the FM Eu-terminated surface. This result has never been seen before, is challenging to predict, but apparently can be
highly interesting and relevant for technological applications.
Authors: Denis Vyalikh et al.
References
- M. Güttler, A. Generalov, S. I. Fujimori, K. Kummer, A. Chikina, S. Seiro, S. Danzenbächer, Yu. M. Koroteev, E. V. Chulkov, M. Radovic, M. Shi, N. C. Plumb, C. Laubschat, J. W. Allen, C. Krellner, C. Geibel & D. V. Vyalikh (2019) Divalent EuRh2Si2 as a reference for the Luttinger theorem and antiferromagnetism in trivalent heavy-fermion YbRh2Si2 Nature Communications doi: 10.1038/s41467-019-08688-y ↩