The role of topology in Faraday’s laws of electrolysis

Any person with some basic knowledge of chemistry is familiar with the concept of electrolysis, i.e., the production of a chemical reaction by passing an electric current through an electrolyte – a liquid that conducts electricity as a result of the presence of ions. It has found major applications since the early days of modern chemistry; thus, for example, William Nicholson and Anthony Carlisle, using the newly developed voltaic battery, performed in 1800 the first electrolysis of water, reversing earlier experiments that showed that hydrogen and oxygen combine to form water.

In electrolysis, positive ions migrate to the cathode and negative ions to the anode. The reactions occurring depend on electron transfer at the electrodes and are therefore redox reactions. At the anode, negative ions in solution may lose electrons to form neutral species. Alternatively, atoms of the electrode can lose electrons and go into solution as positive ions. In either case the reaction is an oxidation. At the cathode, positive ions in solution can gain electrons to form neutral species. Thus, cathode reactions are reductions.

But, even before the concept of atom was firmly established or that of electron was even dreamed of, electrolysis was a reliable and established technique. In 1807, Humphry Davy constructed the most powerful electric battery to that time and began to perform electrolysis on available materials. Metallic potassium emerged easily from molten potash and metallic sodium from lye. The next year Davy used improved methods to obtain the first samples of barium, calcium, magnesium, and strontium.

In 1834, the laws of electrolysis were formulated by Faraday, who had been an assistant to Davy, and can be found in any general chemistry textbook. The laws say, in Faraday’s terms:

1. The amount of chemical change produced is proportional to the quantity of electricity passed.
2. The amount of chemical change produced in different substances by a fixed quantity of electricity is proportional to the electrochemical equivalent of the substance.

Electrolysis is, therefore, a solid pillar of modern chemistry, an accessible and useful concept for the beginner, and an everyday tool for the industrialist. It would seem that, from the theoretical point of view, few things are left to say about a more than 200-year-old household concept. Except, perhaps, that you can’t truly understand its fundamentals without topology.

Faraday’s first law of electrolysis addresses insulating liquids in electrolytic cells and can be recast in modern terms as follows: When a macroscopic number N of nuclei of a given chemical species passes from one electrode to the other, the transported electrical charge is an integer multiple of N times e. The law is additive: it concerns each different chemical species in the cell independently. It addresses ionic conduction in electrolytes, including molten salts, as we have seen; it does not apply to metallic conduction, which is unrelated to the motion of nuclei. On the other hand, Faraday’s “equivalent numbers” can be regarded as the archetypical definition of oxidation numbers (also known as oxidation states) in insulating liquids.

In modern chemistry, the oxidation number of an atom in a molecule or in a solid is an integer determined, importantly, by an agreed set of rules. Nowadays, we know that solids and liquids are not assemblies of ions; they are assemblies of atoms, having ionic character only because neighbouring atoms have different electronegativities. It follows that a lot of different electronegativity scales and/or definitions of atomic charges could be proposed. None of the tens of them already published yields integer values.

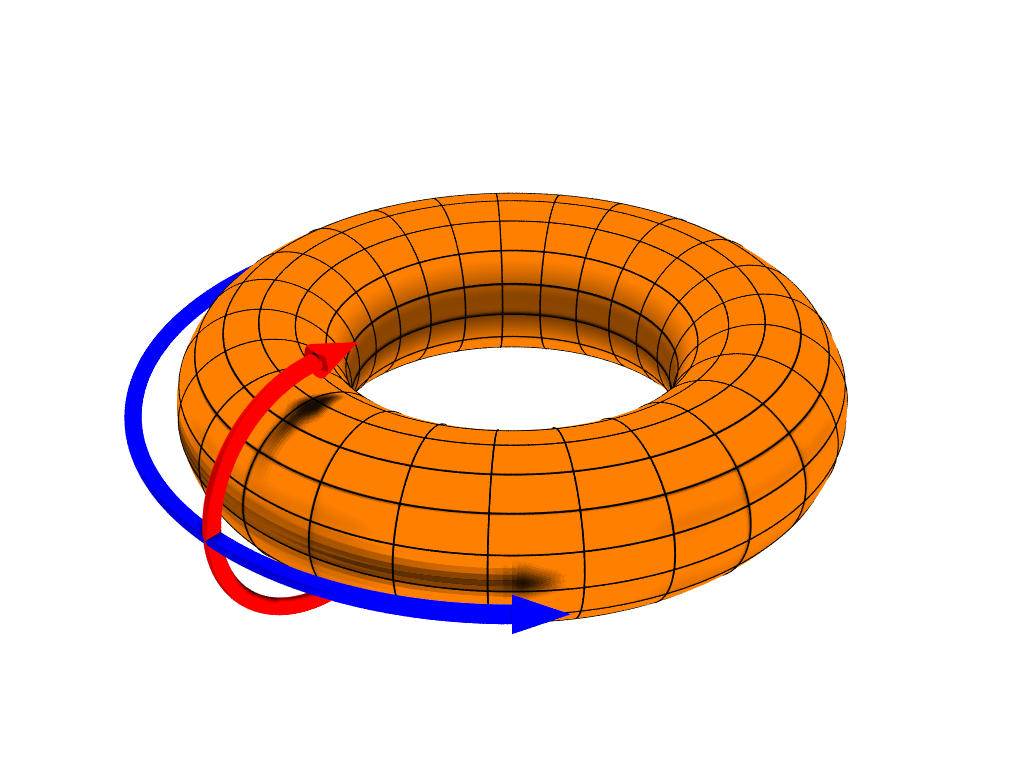
So, how come integer oxidation numbers in electrolytes are measurable quantities since the times of Faraday? The answer is to be found in a playground where topology– as David J. Thouless‘ paper “Quantization of particle transport” (1983) hinted ¹–has a major role.

The main message from topology is that the ionic charges behave as an integer only when adiabatically transported in a macroscopic system; no trace of quantization may appear in a “snapshot” of either a solid or a liquid at a given time. The quantized charge transport may occur either in a real experiment (as in Faraday’s) or in a “gedanken” experiment, nowadays called a “Thouless pump”, an adiabatic quantum motor.

The existing literature deals with the above issues by adopting the independent-electron framework; now, Raffaele Resta provides ² the many-body generalization of all them.

Resta starts from considering electrolytic cells as Thouless pumps. The electrons in the liquid can be described by means of a finite (and closed) quantum system: in order to account for direct steady-state currents, it is then mandatory to adopt periodic boundary conditions. This periodicity resolves in a system that comprises a central cell and its replicas in infinite number, thus acquiring the topology of a torus. One cycle of the pump consists in adiabatic transporting one nucleus from a given position in the central cell to its replica position in the nearby cell, thus making one loop around the torus. Resta shows, with compact and very transparent notations and formulas, that because of topological reasons, an integer electronic charge is pumped.

Author: César Tomé López is a science writer and the editor of Mapping Ignorance

Disclaimer: Parts of this article may have been copied verbatim or almost verbatim from the referenced research paper/s.