Validity of the Kibble-Zurek mechanism for Ising domains
Phase transitions and their related phenomena lie at the core of modern statistical mechanics and condensed matter physics. At equilibrium, an intriguing aspect of second-order phase transitions is that systems with distinct order parameters can be described by the same set of static critical exponents, a hallmark of universality.
Thomas Kibble’s research on phase transitions and topological defects is most significant in this respect. Actually, the Kibble-Zurek mechanism (KZM) is a paradigmatic theory to describe the dynamics across both classical continuous phase transitions and quantum phase transitions.
The dynamical aspect of phase transitions away from equilibrium, such as the formation of intriguing topological defects and domain structures, is much more elusive. KZM describes the non-equilibrium dynamics and the formation of topological defects in a system which is driven through a continuous phase transition at finite rate. It is named after Kibble, who pioneered the study of domain structure formation in the early universe, paving the way to testing cosmological principles in the laboratory, and Wojciech H. Zurek, who related the number of defects it creates to the critical exponents of the transition and to how quickly the critical point is traversed. KZM predicts that the density of topological defects should obey a power-law relation.
Though possible, the search for ideal systems to test KZM remains challenging. To date, aspects of KZM have been experimentally examined in various systems such as superfluid 4He, superconductors, liquid crystals, trapped ions, and Bose-Einstein condensates. KZM has been succesfully verified in a wide variety of physical systems, finding applications from structure formation in the early universe to condensed matter systems. However, whether topologically-trivial Ising domains, one of the most common and fundamental types of domains in condensed matter systems, also obey the KZM has never been investigated in the laboratory.
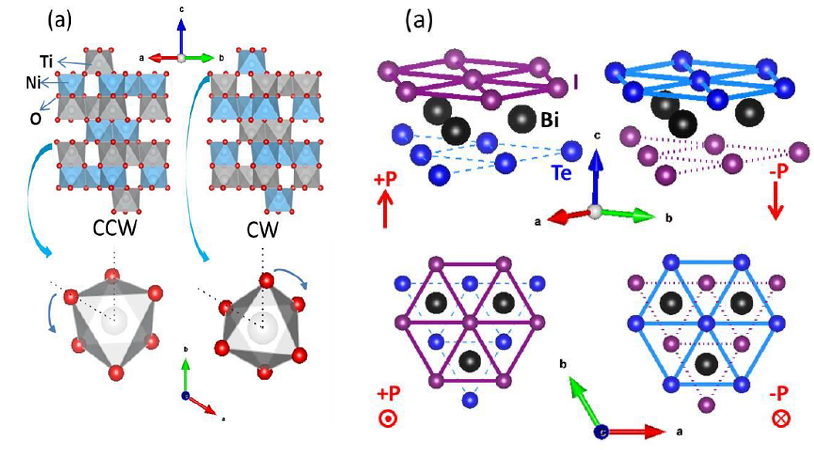
Now, a team of researchers has examined 1 two different kinds of three-dimensional structural Ising domains: clockwise/counter-clockwise ferro-rotation domains in NiTiO3 and up/down polar domains in BiTeI.
The scientists find that While the KZM slope of ferro-rotation domains in NiTiO3 agrees well with the prediction of the 3D Ising model, the KZM slope of polar domains in BiTeI surprisingly far exceeds the theoretical limit, setting an exotic example where possible weak long-range dipolar interactions play a critical role in steepening the KZM slope of non-topological quantities.
These results demonstrate the validity of KZM for Ising domains and reveal an enhancement of the power-law exponent and a possible reduction of the dynamic critical exponent for transitions with long-range interactions.
Author: César Tomé López is a science writer and the editor of Mapping Ignorance
Disclaimer: Parts of this article may have been copied verbatim or almost verbatim from the referenced research paper/s.
References
- Kai Du, Xiaochen Fang, Choongjae Won, Chandan De, Fei-Ting Huang, Wenqian Xu, Hoydoo You, Fernando J. Gómez-Ruiz, Adolfo del Campo & Sang-Wook Cheong (2023) Kibble–Zurek mechanism of Ising domains. Nat. Phys. doi: 10.1038/s41567-023-02112-5 ↩