Triangulations are rigid. You can do better using pseudo-triangles

Triangles are, definitely, among the most used mathematical objects. One of the reasons is that they are simple (actually the smallest polygon). Another very important reason is that they are rigid, which is the property behind the many structures composed by triangles we can see in our daily life.

But, surprisingly enough, triangulations are not the 2D rigid structures with fewest bars. Such structures are the so-called pointed pseudo-triangulations.

Pseudo-triangles generalize the notion of triangle by allowing its sides to be, instead of a single segment, a polygonal chain with the property of being inner convex. Hence, triangles are just a particular, “straight”, type of pseudo-triangles.

Thus, a pseudo-triangulation of a point set is a tessellation of its convex hull by pseudo-triangles. Further, a pseudo-triangulation is said to be pointed if all the vertices are incident to an angle greater than 180 degrees ( for the sweet ones). The following figure shows, for the same set of points, a triangulation (left) and a pointed pseudo-triangulation (right).

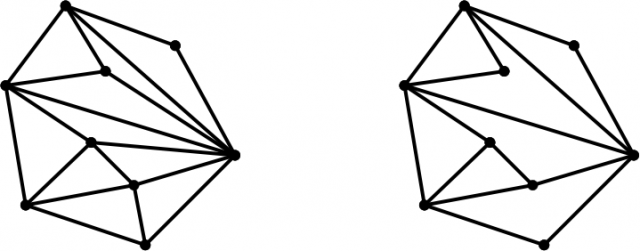
It is apparent that pointed pseudo-triangulations have fewer edges than triangulations. Actually, Streinu ¹ showed that for points a pseudo-triangulation has edges, with being the number of non-pointed vertices. In particular, a pointed pseudo-triangulation has edges, while a triangulation has edges, for being the number of hull points of the set (the only pointed ones in a triangulation).

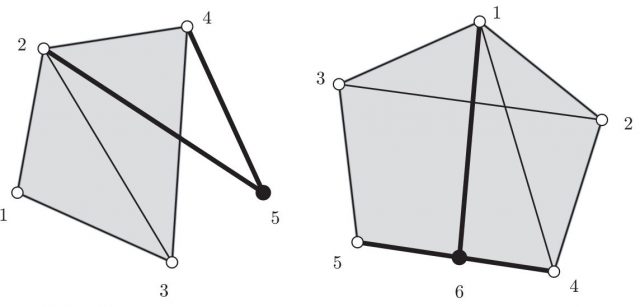
Back to rigidity, and informally speaking, we can say that a structure is rigid if any movement either breaks the structure or moves the structure as a whole. For an example, a triangle is rigid while a pseudo-triangle might not be rigid; the following figure (right) shows a movement which neither breaks the pseudo-triangle nor moves it as a whole.

Streinu also proved that, nicely enough considering the previous example, pointed pseudo-triangulations are rigid. The left picture in the following figure shows that the previous movement now will move the pointed pseudo-triangulation as a whole, as any other movement will do. (Remember that we are working in 2D, so that 3D movements are not allowed.) The reader can figure out the same property for the larger pointed pseudo-triangulation in the right picture.

This implies that, in order to construct a rigid 2D structure, pointed pseudo-triangulations allow to get rid of many bars with respect to triangulations. In particular, as we have seen above, a pointed pseudo-triangulation will use only bars, instead of the bars used by a triangulation.

Streinu also proved that pointed pseudo-triangulations are, in fact, minimally rigid. That is, removing any edge would destroy the rigidity. This is very close to proving that is the smallest number of bars we can use for a rigid 2D structure… except that we have to make sure that there are no other minimally rigid structures.

This was precisely the result by Haas et al.². There we proved that, if a structure is minimally rigid, then it has to be a pointed pseudo-triangulation. More precisely, if an abstract graph is planar (2D structures have no crossings) and minimally rigid, then it can be geometrically embedded as a pointed-pseudo-triangulation.

Interestingly enough, abstract graphs being minimally rigid can be characterized in a purely combinatorial way. Just counting vertices and edges! Laman³ proved that a graph with vertices is minimally rigid if, and only if, (i) it has edges and (ii) every subgraph with vertices has at most edges.

An equivalent way of characterizing the graphs with this property is, as proved by Tay and Whiteley ⁴, the Henneberg construction ⁵:

Start with an edge joining two vertices. At each step, add a new vertex in one of these two ways:

• Henneberg I (vertex addition): insert a new vertex and connect it to two old vertices, using two new edges.

• Henneberg II (edge splitting): insert a new vertex on an old edge, which gets split into two new edges, and connect the new vertex to a third old vertex, using one new edge.

Our first proof technique, of a local nature, shows that there are geometric placements of the points in this abstract Henneberg which result in an embedding of the minimally rigid planar graph meeting the conditions a pointed pseudo-triangulation (pointedness and pseudo-triangles as faces).

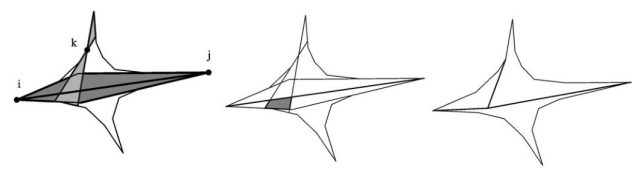
Our second proof technique, of a global nature, makes use of a directed version of Tutte’s barycentric embedding ⁶, adapted to produce pointed-pseudo-triangulations instead of convex faces.

Both proofs yield efficient embedding algorithms and allow to obtain some stronger results, using a combinatorial abstraction of pseudo-triangulations. These combinatorial pseudo-triangulations are defined as topological plane embeddings of a graph, together with an assignment of angles which mimics the properties of geometric pseudo-triangulations.

Using this notion, part of the authors of [2] could further generalize the previous results to general rigidity and pseudo-triangulations ⁷. Actually, we showed that the rigidity of planar graphs can be stratified according to the number of non-pointed vertices in an associated combinatorial pseudo-triangulation.

In summary, apart from having other interesting properties, pseudo-triangulations provide a missing link between planarity and rigidity in geometric graph theory.