Always look on the light side of graphs
Consider a set of ![]() distinct points in the plane, no three of them on the same line. Draw straight-line segments joining pairs of those points. This is called a geometric graph
distinct points in the plane, no three of them on the same line. Draw straight-line segments joining pairs of those points. This is called a geometric graph ![]() and here we are going to focus on the segments of such a graph.
and here we are going to focus on the segments of such a graph.

Every segment has two sides, defined by the line in which it is contained. Such a side is said to be a light side if it does not contain, totally, any other segment. Note that the sides are considered to be open, excluding the line.
Next, a segment is said to be a light segment if it has a light side. Finally, a geometric graph is a light graph if all of its segments are light segments.
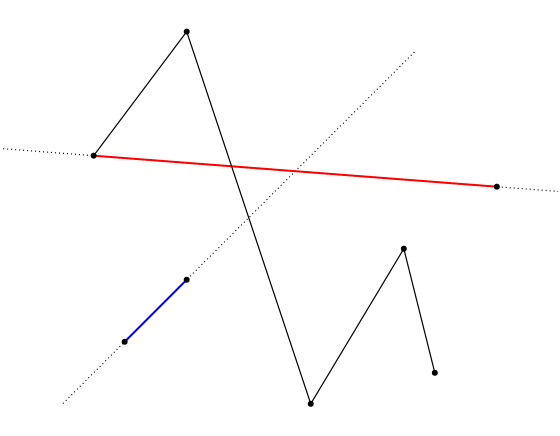
In this figure, the red segment is light, because its upper side is light. Note that there is a segment sharing a point with the red one; since the sides exclude the line, that segment is not totally contained in the upper side. On the contrary, the blue segment is not light because both sides contain, totally, some segment and, therefore, the blue segment has no light side. Hence, the graph is not a light graph.
Now suppose that you are given a number ![]() and you are asked to draw as many light segments as possible on
and you are asked to draw as many light segments as possible on ![]() points. How many light segments can you draw? In other words:
points. How many light segments can you draw? In other words:
Which is the maximum possible number of segments in a light graph?
A bound is given by Ackerman et al. 1, who provide an easy-to-read proof showing that:
A light geometric graph on
points has at most
segments.
The problem can be generalized, by allowing a certain number of segments to be contained in a light side. Hence, a ![]() -light side contains, totally, at most
-light side contains, totally, at most ![]() segments. Following the lines of the original problem, a segment is said to be a
segments. Following the lines of the original problem, a segment is said to be a ![]() -light segment if it has a
-light segment if it has a ![]() -light side. Finally, a geometric graph is a
-light side. Finally, a geometric graph is a ![]() -light graph if all of its segments are
-light graph if all of its segments are ![]() -light segments.
-light segments.
Again, if you are given a number ![]() and you want to draw as many
and you want to draw as many ![]() -light segments as possible on
-light segments as possible on ![]() points, how many can you draw? Equivalently:
points, how many can you draw? Equivalently:
Which is the maximum possible number of segments in a
-light graph?
Ackerman et al. also show a bound for this generalized case, using the previous one (which, in fact, is that of ![]() -light graphs) together with a probabilistic argument. Their result says that:
-light graphs) together with a probabilistic argument. Their result says that:
A
-light geometric graph on
points has at most
segments.
Asymptotically this gives ![]() segments, which is also shown to be the best answer possible. Consider
segments, which is also shown to be the best answer possible. Consider ![]() points forming a regular polygon and connect with a segment those points whose cyclic distance is at most
points forming a regular polygon and connect with a segment those points whose cyclic distance is at most ![]() . This gives a
. This gives a ![]() -light geometric graph with
-light geometric graph with ![]() edges.
edges.
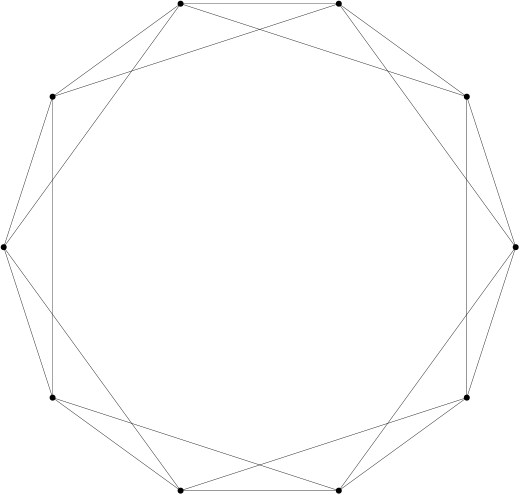
The figure shows the case with ![]() and
and ![]() , in which the
, in which the ![]() edges are light.
edges are light.
It is interesting to know that the paper cited above extends a previous result by Ackerman and Pinchasi 2. There, they studied a stronger problem, considering general lines ![]() instead of segments. A
instead of segments. A ![]() -light side of a line is defined in a similar manner and, thus,
-light side of a line is defined in a similar manner and, thus, ![]() -light lines are those having a light side. A geometric graph is said to be a
-light lines are those having a light side. A geometric graph is said to be a ![]() -near bipartite graph if every line
-near bipartite graph if every line ![]() is a
is a ![]() -light line with respect to the graph.
-light line with respect to the graph.
Since ![]() -light graphs are a particular case of
-light graphs are a particular case of ![]() -near bipartite graphs, in which only segments and not general lines
-near bipartite graphs, in which only segments and not general lines ![]() are considered, the bound provided for
are considered, the bound provided for ![]() -light graphs applies as well to
-light graphs applies as well to ![]() -near bipartite graphs.
-near bipartite graphs.
Before finishing, let us mention another concept related to that of light segments. Two segments are said to be avoiding segments if no line containing one of them intersects the other. Equivalently, two segments are avoiding if they are opposite edges of a convex quadrilateral.
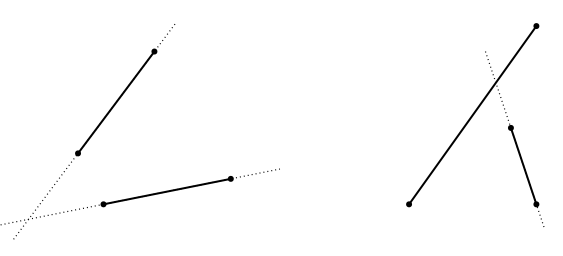
The figure shows a pair of avoiding segments (left) and a pair of segments which are not avoiding (right). For a connection between this notion and the previous one, observe that a light segment has a side not containing segments and, hence, it can only avoid those segments totally contained in the heavy side (or should we call it the dark side?)
The notion of avoiding segments was introduced by Kupitz 3, who conjectured that:
Any geometric graph on
points which does not contain a pair of avoiding segments has at most
edges.
The conjecture was proved to be true some years later by Valtr 4. The techniques used there can be applied, as well, to deduce an upper bound for the maximum number of segments in a light geometric graph. Nevertheless, the constant obtained in that way is different than the one showed by Ackerman et al.
Finally, let me finish by encouraging you to explore this notions by making your own drawings. For instance, draw some set of ![]() points and try to draw on it as many light segments as possible. And, remember, always look on the light side!
points and try to draw on it as many light segments as possible. And, remember, always look on the light side!

References
- Eyal Ackerman, Jacob Fox, Rom Pinchasi. A note on light geometric graphs. Discrete Mathematics 313 (2013) 1281-1283. DOI: http://dx.doi.org/10.1016/j.disc.2013.03.001 ↩
- Eyal Ackerman, Rom Pinchasi. On the light side of geometric graphs. Discrete Mathematics 312 (2012) 1213-1217. DOI: http://dx.doi.org/10.1016/j.disc.2011.12.009 ↩
- Yakov Shimeon Kupitz. On pairs of disjoint segments in convex position in the plane. Annals of Discrete Mathematics 20 (1984) 203-208. DOI: http://dx.doi.org/10.1016/S0304-0208(08)72827-5 ↩
- Pavel Valtr. On geometric graphs with no
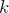 pairwise parallel edges. Discrete and Computational Geometry 19 (3) (1998) 461-469. DOI: http://dx.doi.org/10.1007/PL00009364 ↩
pairwise parallel edges. Discrete and Computational Geometry 19 (3) (1998) 461-469. DOI: http://dx.doi.org/10.1007/PL00009364 ↩
2 comments
[…] entrada está basada en la entrada Always look on the light side of graphs, que escribí para Mapping Ignorance. Si no conoces ese blog de divulgación científica, te invito […]
I will immediately clutch your rss as I can’t to find your e-mail subscription hyperlink or newsletter service. Do you’ve any?
Kindly allow me understand in order that I may just subscribe.
Thanks.