Progress checking Zarankiewicz’s conjecture on the brick factory problem
A previous post presented the fascinating history of the brick factory problem, which wonders about the smallest possible number of rail crossings when connecting ![]() kilns and
kilns and ![]() storage yards1, which is mathematically modeled by the crossing number of the complete bipartite graph
storage yards1, which is mathematically modeled by the crossing number of the complete bipartite graph ![]() .
.

Proposed by Paul Turán after the Second World War, the first advances on this problem arose in 1952, due to the probabilist Kazimierz Urbanik and the topologist Kazimierz Zarankiewicz. The latter claimed to have solved the problem, stating that the smallest possible number of crossings ![]() was
was ![]() and proposing a simple way of attaining this number.
and proposing a simple way of attaining this number.
It would be enough to (1) draw the ![]() vertices on the x-axis, split as evenly as possible among the strictly positive and the strictly negative semi-axes, (2) proceed analogously with the
vertices on the x-axis, split as evenly as possible among the strictly positive and the strictly negative semi-axes, (2) proceed analogously with the ![]() vertices on the y-axis, and (3) use straight-line segments to join pairs of vertices lying on different axes.
vertices on the y-axis, and (3) use straight-line segments to join pairs of vertices lying on different axes.
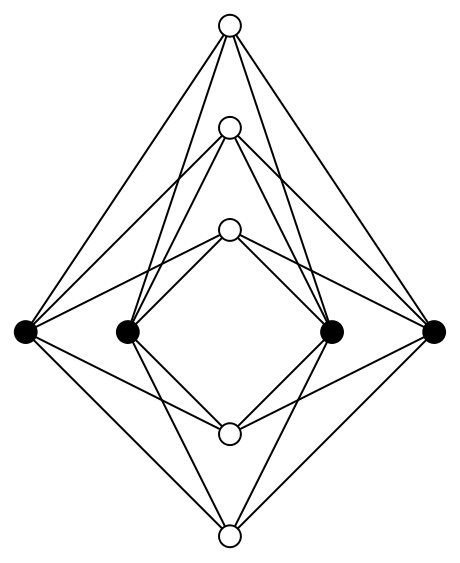
Unfortunately, the proof was found to be incorrect around 1965 2 and, more than sixty years later, Zarankiewicz’s conjecture remains one of the most tantalizing open problems in graph theory.
During these years, some advances have been achieved checking the conjecture for a few values. Zarankiewicz’s proof3, published in 1952, did work for the case ![]() . A paper by Kleitman4, in 1970, extended the validity to
. A paper by Kleitman4, in 1970, extended the validity to ![]() and Woodall5, in 1993, checked the cases
and Woodall5, in 1993, checked the cases ![]() and
and ![]() with the help of computers.
with the help of computers.
The aim of this post is to introduce a different kind of progress on checking Zarankiewicz’s conjecture, presented by Christian et al. 6 in a recent paper. For each fixed ![]() , the authors manage to determine an integer
, the authors manage to determine an integer ![]() (depending on
(depending on ![]() ) such that:
) such that:
If Zarankiewicz’s conjecture holds for the fixed
together with all
,
then it holds for that
together with every
.
In other words, what this paper shows is that, for a given ![]() , checking Zarankiewicz’s conjecture reduces to checking a finite number of values for
, checking Zarankiewicz’s conjecture reduces to checking a finite number of values for ![]() (which is in turn a finite problem). But do not start shouting about it. It turns out that the method is not practical even for
(which is in turn a finite problem). But do not start shouting about it. It turns out that the method is not practical even for ![]() .
.
The expression of ![]() obtained by the authors is
obtained by the authors is
,
where ![]() (note that this is the part using
(note that this is the part using ![]() in the expression for Zarankiewicz’s conjecture).
in the expression for Zarankiewicz’s conjecture).
This means that ![]() , a really big number. The fastest computers today perform in the order of petaFLOPS (
, a really big number. The fastest computers today perform in the order of petaFLOPS (![]() operations per second), so even if they could check each case in a single operation, it would take in the order of
operations per second), so even if they could check each case in a single operation, it would take in the order of ![]() years to check if the conjecture holds for
years to check if the conjecture holds for ![]() with all
with all ![]() .
.
Nevertheless, the result is a remarkable progress in such a tantalizing problem. Although giving full details about the proofs is certainly out of the scope of this post, we can outline the arguments used by Christian et al. In order to do so, we just need to introduce two notions about drawings of ![]() .
.
Consider the vertices in the two classes of the bipartite graph (white and black points in the previous figure) labeled as ![]() and
and ![]() . Before introducing the first notion observe that, in any drawing, each vertex
. Before introducing the first notion observe that, in any drawing, each vertex ![]() of the second class induces a natural cyclic order of
of the second class induces a natural cyclic order of ![]() , just considering the clockwise cyclic order of the edges incident to it. This cyclic order is the rotation of the vertex in the drawing. The following figure shows a rotation
, just considering the clockwise cyclic order of the edges incident to it. This cyclic order is the rotation of the vertex in the drawing. The following figure shows a rotation ![]() .
.
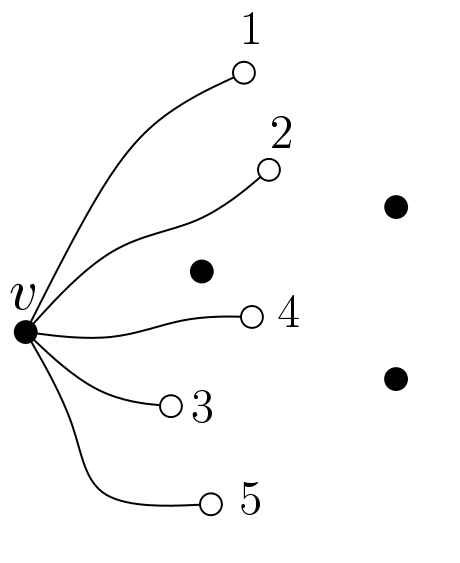
Note that there are ![]() possible rotations for a vertex of degree
possible rotations for a vertex of degree ![]() , since this is the number of cyclic permutations of
, since this is the number of cyclic permutations of ![]() .
.
The second notion is what Christian et al. call templates. A drawing of ![]() is defined to be a template of rank
is defined to be a template of rank ![]() and order
and order ![]() if there are no two vertices of degree
if there are no two vertices of degree ![]() having the same rotation. The authors show that, for each positive integer
having the same rotation. The authors show that, for each positive integer ![]() , there is an optimal drawing of
, there is an optimal drawing of ![]() that can be obtained (1) from some template of rank
that can be obtained (1) from some template of rank ![]() and order
and order ![]() (2) by duplicating vertices of degree
(2) by duplicating vertices of degree ![]() in the template, and (3) so that the crossing number of the resulting optimal drawing of
in the template, and (3) so that the crossing number of the resulting optimal drawing of ![]() can be determined by information contained in the template and the distribution of the duplicate vertices.
can be determined by information contained in the template and the distribution of the duplicate vertices.
A key fact is that, up to isomorphism, the number of templates to consider turns out to be finite.
Then, the authors associate a quadratic program to each template, in such a way that the minimum of the quadratic program provides information about whether, for this template, a drawing of ![]() obtained as above is a counterexample to Zarankiewicz’s conjecture.
obtained as above is a counterexample to Zarankiewicz’s conjecture.
In summary, although not being practical today, the paper by Christian et al. opens a way towards checking Zarankiewicz’s conjecture for a given value of ![]() . Furthermore, it remarkably finds its place in the list of very few results around this conjecture in the last sixty years.
. Furthermore, it remarkably finds its place in the list of very few results around this conjecture in the last sixty years.
References
- Lowell Beineke and Robin Wilson. The Early History of the Brick Factory Problem. The Mathematical Intelligencer. Volume 32, Issue 2 (June 2010), pages 41-48. http://dx.doi.org/10.1007/s00283-009-9120-4. ↩
- Richard K. Guy. The decline and fall of Zarankiewicz’s theorem. In: Proof Techniques in Graph Theory (ed. F. Harary), New York: Academic Press (1969), pages 63–69. ↩
- K. Zarankiewicz. On a problem of P. Turan concerning graphs. Fundamenta Mathematicae. Volume 41 (1954), pages 137–145. ↩
- Daniel J. Kleitman. The crossing number of
 . Journal of Combinatorial Theory. Volume 9 (1970), pages 315–323. http://dx.doi.org/10.1016/S0021-9800(70)80087-4 ↩
. Journal of Combinatorial Theory. Volume 9 (1970), pages 315–323. http://dx.doi.org/10.1016/S0021-9800(70)80087-4 ↩ - Douglas R. Woodall, Cyclic-order graphs and Zarankiewicz’s crossing-number conjecture, Journal of Graph Theory. Volume 17, Issue 6 (December 1993), pages 657–671. http://dx.doi.org/10.1002/jgt.3190170602 ↩
- Christian R., Richter R.B. & Salazar G. (2013). Zarankiewiczʼs Conjecture is finite for each fixed m, Journal of Combinatorial Theory, Series B, 103 (2) 237-247. DOI: 10.1016/j.jctb.2012.11.001 ↩
1 comment
[…] escribí para Mapping Ignorance y que llegó hasta reddit. En el mismo blog, en la entrada Progress checking Zarankiewicz’s conjecture on the brick factory problem, puedes encontrar algunos progresos recientes relacionados con este problema. Aunque no han […]